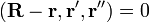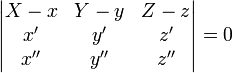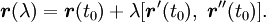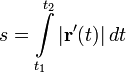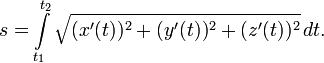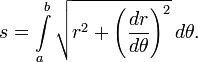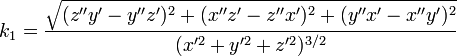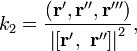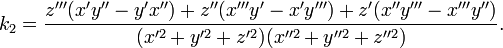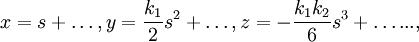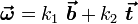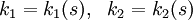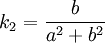что такое длина кривой

Длина дуги кривой

Дифференциальная геометрия кривых — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами.

Содержание

Способы задания кривой

Наиболее общий способ задать уравнение пространственной кривой — параметрический:

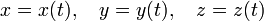(1),

Часто удобно использовать инвариантную и компактную запись уравнения кривой с помощью вектор-функции:

,

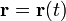
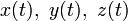
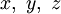
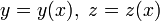
В зависимости от свойств дифференцируемости функций , задающих кривую, говорят о степени гладкости (регулярности) кривой. Кривая называется регулярной, если для любой её точки, при подходящем выборе прямоугольной декартовой системы координат , она допускает в окрестности этой точки задание уравнениями вида:

,

где y(x) и z(x) — дифференцируемые функции.

Для того чтобы точка кривой, заданной общим уравнением (1), была обыкновенной (не особой точкой), достаточно, чтобы в этой точке выполнялось вышеуказанное неравенство

Дифференциальная геометрия рассматривает также кусочно-гладкие кривые, которые состоят из гладких участков, разделённых особыми точками. В особых точках определяющие функции либо не удовлетворяют условиям регулярности, либо вообще не дифференцируемы.

Плоские кривые

Важный класс кривых представляют плоские кривые, то есть кривые, лежащие в плоскости. Плоскую кривую также можно задать параметрически, первыми двумя из трёх уравнений (1). Другие способы:

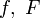
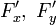
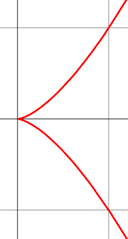
Функции предполагаются непрерывно дифференцируемыми. При неявном задании точка кривой будет обыкновенной, если в её окрестности функция F(x,y) имеет непрерывные частные производные , не равные нулю одновременно.

Приведём примеры особых точек для плоских кривых.

Соприкосновение

при ,

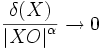
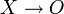
В применении к кривым это означает следующее: две кривые в общей точке имеют степень касания не ниже k-го порядка, если их производные в общей точке, до k-го порядка включительно, совпадают.

Касательная

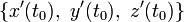
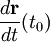
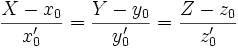
Гладкая регулярная кривая в каждой точке имеет определённую касательную. Направление касательной в точке t₀ кривой, задаваемой уравнениями (1), совпадает с направлением вектора . В векторной записи это производная .

,

Для плоской кривой уравнение касательной в точке 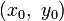имеет следующий вид.

Соприкасающаяся плоскость и нормали

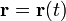
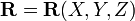
Пусть — уравнение кривой. Тогда уравнение её соприкасающейся плоскости определяется из соотношения:

В координатах оно имеет вид:

Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью.

Направление главной нормали может быть получено как двойное векторное произведение: .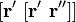

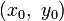
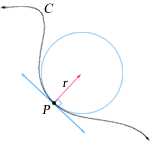
Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке имеет следующий вид.

Соприкасающаяся окружность

Центр соприкасающейся окружности называют центром кривизны, а радиус — радиусом кривизны. Радиус кривизны является величиной, обратной кривизне (см. ниже). Центр соприкасающейся окружности всегда лежит на главной нормали; отсюда следует, что эта нормаль всегда направлена в сторону вогнутости кривой.

Геометрическое место центров кривизны кривой называется эволютой. Кривая, ортогонально пересекающая касательные кривой, называется эвольвентой. Построение эволюты и эвольвенты — взаимно обратные операции, то есть для эвольвенты данной кривой эволютой является сама кривая.

Длина дуги кривой

Для измерения длины участка (дуги) произвольной кривой эта кривая заменяется ломаной, содержащей точки кривой как точки излома, и максимум длин всех таких ломаных принимается за длину кривой (рис. 3). В инвариантном виде формула для вычисления длины дуги (спрямления кривой) имеет вид:

То же в декартовых координатах:

В полярных координатах для плоской кривой:

Параметризация

Кривая допускает бесчисленное множество различных способов параметрического задания уравнениями вида (1). Среди них особое значение имеет так называемая естественная параметризация, когда параметром служит длина дуги кривой, отсчитываемая от некоторой фиксированной точки.

Среди преимуществ такой параметризации:

Кривизна

При движении вдоль кривой её касательная меняет направление. Скорость этого вращения при равномерном, с единичной скоростью, движении вдоль кривой называется кривизной кривой. В случае параметрического задания кривой уравнениями (1) кривизна кривой определяется по формуле

,

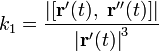
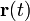
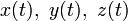
где — вектор-функция с координатами .

Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость.

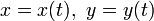
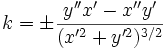
Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения. Кривизна плоской кривой, задаваемой уравнениями , определяется по формуле

.

Кручение

При движении вдоль кривой в окрестности заданной точки соприкасающаяся плоскость вращается, причём касательная к кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении называется кручением. Направление вращения определяет знак кручения.

Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определённое кручение. В случае параметрического задания кривой уравнениями (1) кручение кривой определяется по формуле

Для прямой кручение не определено, поскольку неоднозначно определяется соприкасающаяся плоскость. Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением — плоская.

Формулы Френе

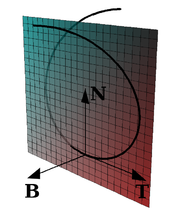
Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе, см. рис. 4). Соприкасающаяся и нормальная плоскости уже упоминались; третья плоскость, содержащая касательную и бинормаль, называется спрямляющей.

Если рёбра естественного трёхгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации раскладывается в окрестности этой точки в ряд по координате вдоль кривой:

где k₁ и k₂ — кривизна и кручение кривой в указанной точке.

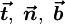
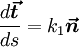Единичные векторы , соответственно для касательной, главной нормали и бинормали кривой, при движении вдоль кривой изменяются. При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы:

(2)

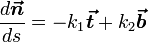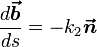где дифференцирование идёт по дуге кривой. Формулы (2) называют формулами Френе́, или Френе-Серре.

Кинематическое истолкование

Будем рассматривать длину дуги заданной кривой как время, а трёхгранник Френе — как твёрдое тело, движущееся вдоль кривой. Тогда это движение в каждый момент времени состоит из поступательного (вдоль касательной) и мгновенного вращения с угловой скоростью 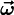(вектор Дарбу). Из формул Френе вытекает:

Это означает, что вектор мгновенного вращения лежит в спрямляющей плоскости и распадается на 2 составляющие: вращение вокруг бинормали со скоростью k₁ (поворот) и вращение вокруг касательной со скоростью k₂ (кручение).

Натуральные уравнения кривой

Кривая с отличной от нуля кривизной полностью определяется (с точностью до положения в пространстве) заданием её кривизны и кручения как функций дуги s кривой. В связи с этим систему уравнения

называют натуральными уравнениями кривой.

Пример

Рассмотрим винтовую линию (рис. 4), заданную уравнениями:

z(t) = bt

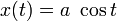
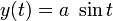
По вышеприведенным формулам получаем:

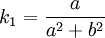
Таким образом, кривизна и кручение винтовой линии постоянны. Поскольку натуральные уравнения однозначно определяют форму кривой, других кривых с постоянными кривизной и кручением не существует. Предельными случаями винтовой линии являются окружность (она получается при b = 0 ) и прямая ( a = 0 ).

См. также

Литература

Полезное

Смотреть что такое «Длина дуги кривой» в других словарях:

Длина дуги — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия

Длина кривой — (или, что то же, длина дуги кривой) в метрическом пространстве числовая характеристика протяжённости этой кривой[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой… … Википедия

ДЛИНА — 1) Длина отрезка прямой расстояние между его концами.2) Длина ломаной сумма длин ее звеньев.3) Длина дуги кривой предел длины вписанной в нее ломаной, когда число ее звеньев неограниченно возрастает, причем длина каждого звена стремится к нулю … Большой Энциклопедический словарь

ДЛИНА — числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. Длина ломаной сумма Д. ее звеньев. Д. простой дуги точная верхняя грань… … Математическая энциклопедия

ДЛИНА — числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. Длина ломаной сумма Д. ее звеньев. Д. простой дуги точная верхняя грань… … Математическая энциклопедия

ДЛИНА — физ. величина, характеризующая протяжённость, удалённость и перемещение тел или их частей вдоль заданной линии. Единица измерения в СИ метр (м). Д. отрезка прямой расстояние между его концами. Д. дуги ломаной сумма длин её прямолинейных звеньев.… … Естествознание. Энциклопедический словарь

Длина — Размерность L Единицы измерения СИ м СГС см … Википедия

Длина — числовая характеристика протяжённости линий. В разных случаях понятие Д. определяется различно. 1) Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. 2) Д. ломаной сумма Д. её звеньев.… … Большая советская энциклопедия

Кручение кривой — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия

Источник

Вычисление длин дуг с помощью определённого интеграла. Теория, примеры и рисунки.

Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.

Как вычислить длину кривой

Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).

Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).

Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).

Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

Применим схему I (метод сумм).

2. Длину хорды (или звена ломаной) ΔL 1 можно найти по теореме Пифагора из треугольника с катетами Δx i и Δу i:

По теореме Лагранжа о конечном приращении функции Δу i=ƒ'(с i)•Δх i, где ci є (x i-1;x i). Поэтому

а длина всей ломаной M 0M 1. М n равна

3.Длина l кривой АВ, по определению, равна

Заметим, что при ΔL i → 0 также и Δx i → 0 ΔLi = и, следовательно, |Δx i| i).

Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δx i → 0 :

Таким образом, или в сокращенной записи l =

Если уравнение кривой АВ задано в параметрической форме

где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле

Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,

Длина всей окружности L = 2πr.

(1)

где y ‘ – производная функции y = f(x) по переменной x.

Длина дуги равна сумме длин составляющих ее элементов:

.

.

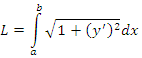Пример 6.

Источник

Вычисление длины кривой

Вычисление длины кривой

Вычисление длины кривой. Мы рассмотрели ряд вопросов, которые приводят к понятию определенных интегралов. Но есть и другой круг проблем, который приводит к понятию определенного интеграла. Они знают скорость изменения 1 суммы на другую величину, и им нужно найти первую величину, точнее, производную функции, но им нужно найти саму функцию, то есть данную функцию. 1 один из его примитивов. Эта задача решается с помощью конкретного интеграла. Это связано с тем, что такие примитивы являются, например, конкретным интегралом с переменной upper bound. As в качестве примера такой задачи рассмотрим расчет длины дуги кривой.

Все они едины в том, что нахождение значения некоторых из этих величин привело к определению предела некоторой интегральной суммы, когда тонкость разбиения стремится к нулю, то есть к определенному интегралу. Людмила Фирмаль

Если интегральная формула длины кривой стремится к нулю гранулярности соответствующего разбиения, то длина может быть выражена не только как верхний предел длины всех возможных пунктирных линий, вписанных на ней, но и как ее предел. Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник