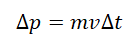что такое импульс системы материальных точек
Что такое импульс системы материальных точек
Найдём скорость `(Delta vecP_(«c»))/(Delta t)` изменения импульса системы материальных точек (ответ на такой вопрос для одной материальной точки нам известен). Для примера рассмотрим систему двух материальных точек. Будем считать, что на первую материальную точку действуют суммарной силой `vecF_1` внешние по отношению к системе тела и внутренняя сила `vecf_(12)` со стороны второго тела. В свою очередь, на вторую материальную точку действуют внешние по отношению к системе тела, сумма этих сил `vecF_2`, и внутренняя сила `vecf_(21)` со стороны первого тела. Тогда с учётом второго закона Ньютона для каждого тела получаем
`(Delta vecP_(«c»))/(Delta t) = (Delta vecp_1)/(Delta t) + (Delta vecp_2)/(Delta t) = (vecF_1 + vecf_(12)) + (vecF_2 + vecf_(21))`.
По третьему закону Ньютона `vecf_(12) + vecf_(21) = vec 0`, и мы приходим к теореме об изменении импульса системы материальных точек
`(Delta vecP_(«c»))/(Delta t) = vecF_1 + vecF_2`,
скорость изменения импульса системы материальных точек равна векторной сумме всех внешних сил, действующих на систему.
Клин массой `M` находится на шероховатой горизонтальной поверхности стола. На клин положили брусок массой `m` и отпустили. Брусок стал соскальзывать, а клин остался в покое. Коэффициент трения скольжения бруска по поверхности клина равен `mu`, наклонная плоскость клина составляет с горизонтом угол `alpha`. Найдите горизонтальную `R_1` и вертикальную `R_2` силы (рис. 9), с которыми клин действует на опору.
По третьему закону Ньютона искомые силы связаны с силой трения `vecR_1 =- vecF_(«тр»` и силой нормальной реакции `vecR_2 =- vecN_(«г»)`, действующими на клин со стороны опоры (рис. 10). Силы `vec(F_sf»тр»)` и `vec(N_sf»г»)`, наряду с силами тяжести, являются внешними по отношению к системе «клин + брусок» и определяют скорость изменения импульса этой системы.
Импульс `vecP_(«c»)` системы направлен по скорости бруска и по величине равен произведению массы бруска на его скорость `vecP_(«c») = vec p = m vec v (t)`. Для определения скорости изменения импульса `vec p` бруска обратимся ко второму закону Ньютона (рис. 11):
`(Delta vecp)/(Delta t) = m vec g + vec N + vec(f_sf»тр»`.
Переходя к проекциям приращений импульса бруска и сил на оси `Oy` и `Ox` с учётом соотношения `f_sf»тр» = mu N`, получаем
По теореме об изменении импульса системы «клин + брусок»
`(Delta vecP_(«c»))/(Delta t) = M vec g + m vec g + vecN_(«г») + vecF_(«тр»)`.
Переходя в последнем равенстве к проекциям на горизонтальное и вертикальное направления с учётом
Отсюда находим искомые силы
Что такое импульс системы материальных точек
В основе динамики материальной точки лежат законы (аксиомы) Ньютона. Напомним ключевые определения и законы.
Система отсчёта, в которой любая материальная точка, не взаимодействующая с другими телами (такая точка называется свободной), движется равномерно и прямолинейно или покоится, называется инерциальной.
инерциальные системы отсчёта (ИСО) существуют
в ИСО приращение импульса материальной точки пропорционально силе и происходит по направлению силы:
`Delta vec p = vec F * Delta t` (1)
Импульсом (или количеством движения) материальной точки называют физическую величину, определяемую произведением её массы на вектор скорости в данной системе отсчёта:
в ИСО приращение импульса материальной точки равно импульсу силы.
Отметим, что при изучении динамики второй закон Ньютона часто формулируют следующим образом:
в ИСО ускорение материальной точки прямо пропорционально сумме сил, действующих на неё, и обратно пропорционально её массе:
Если масса тела остаётся неизменной, то `Delta vec p = Delta (m vec v) = m Delta vec v`, и соотношение (1) принимает вид `m Delta vec v = vec F Delta t`. С учётом `vec a = (Delta vec v)/(Delta t)` приходим к эквивалентности соотношений (1) и (2) в рассматриваемом случае.
В настоящем Задании представлены задачи, для решения которых привлекается второй закон Ньютона (см.(1)), устанавливающий равенство приращений импульса материальной точки и импульса силы.
при взаимодействии двух материальных точек сила `vecF_(12)`, действующая на первую материальную точку со стороны второй, равна по величине и противоположна по направлению силе `vecF_(21)`, действующей со стороны первой материальной точки на вторую:
1) силы возникают парами и имеют одинаковую природу, они приложены к разным материальным точкам,
2) эти силы равны по величине,
3) они действуют вдоль одной прямой в противоположных направлениях.
Заметим, что согласно третьему закону Ньютона обе силы должны быть равны по величине в любой момент времени независимо от движения взаимодействующих тел. Другими словами, если в системе двух взаимодействующих тел изменить положение одного из тел, то это изменение мгновенно скажется на другом теле, как бы далеко оно ни находилось. На самом деле скорость распространения взаимодействий конечная; она не может превзойти скорость света в вакууме. Поэтому третий закон Ньютона имеет определённые пределы применимости. Однако в классической механике при малых скоростях взаимодействующих тел он выполняется с большой точностью.
Второй закон Ньютона (уравнение движения) можно представить в виде теоремы об изменении импульса материальной точки:
Скорость изменения импульса материальной точки в инерциальной системе отсчёта равна сумме сил, действующих на эту точку.
Напомним, что для решения задач динамики материальной точки следует:
привести «моментальную фотографию» движущегося тела, указать приложенные к нему силы;
выбрать инерциальную систему отсчёта;
составить уравнение (3);
перейти к проекциям приращения импульса и сил на те или иные направления;
решить полученную систему.
Рассмотрим характерные примеры.
На рис. 1 показаны ИСО и силы, действующие на тело в процессе разгона. По второму закону Ньютона
`(Delta vec p)/(Delta t) = M vec g + vec N + vecF_(«тр») + vec F`.
Переходя к проекциям на горизонтальную ось, находим элементарные приращения импульса в процессе разгона
и в процессе торможения `(F = 0)`
Просуммируем все приращения импульса тела от старта до остановки:
Далее рассмотрим пример, в котором одна из сил зависит от времени.
Так как `mg в импульсе силы можно интерпретировать как площадь элементарного прямоугольника со сторонами `F(t)` и `Delta t` на графике зависимости `F(t)`). Тогда импульс силы `F` за время удара равен
и в рассматриваемом случае не зависит от того, в какой именно момент времени сила достигает максимального значения (площадь треугольника равна половине произведения основания на высоту!). Далее находим импульс мяча в момент окончания действия силы
Отсюда находим начальную скорость полёта мяча
`v = (F_max * tau)/(2m) = (3,5 * 10^3 * 8 * 10^-3)/(2 * 0,5) = 28 sf»м/с»`
и максимальную дальность (старт под углом `alpha = pi/4`) полёта
В рассматриваемом модельном примере получен несколько завышенный по сравнению с наблюдениями результат.
На вступительных испытаниях и олимпиадах в вузах России регулярно предлагаются задачи динамики, в которых наряду с «традиционными» силами: силой тяжести, силой Архимеда и т. д., на тело действует сила лобового сопротивления. Такая сила возникает, например, при движении тел в жидкостях и газах. Вопрос о движении тел в жидкостях и газах имеет большое практическое значение. Знакомство с действием такого рода сил уместно начинать, как это принято в физике, с простейших модельных зависимостей, в которых сила сопротивления принимается пропорциональной скорости или её квадрату.
Мяч, брошенный с горизонтальной поверхности земли под углом `alpha = 60^@` к горизонту со скоростью `v = 10 sf»м/с»`, упал на землю, имея вертикальную составляющую скорости по абсолютной величине на `delta = 30 %` меньшую, чем при бросании. Найдите время полёта мяча. Считать, что сила сопротивления движению мяча пропорциональна его скорости.
Согласно второму закону Ньютона приращение импульса пропорционально силе и происходит по направлению силы:
Переходя к проекциям сил и приращения скорости на вертикальную ось, получаем
Заметим, что элементарное перемещение мяча по вертикали равно `Delta y = v_y * Delta t`, и перепишем последнее соотношение в виде:
Просуммируем все приращения вертикальной проекции импульса по всему времени полёта, т. е. от `t = 0` до `t = T`:
Переходя к конечным приращениям, получаем
Точки старта и финиша находятся в одной горизонтальной плоскости, поэтому перемещение мяча по вертикали за время полёта нулевое
Кубик, движущийся поступательно со скоростью `v` (рис. 4) по гладкой горизонтальной поверхности, испытывает соударение с шероховатой вертикальной стенкой.
Коэффициент трения `mu` скольжения кубика по стенке и угол `alpha` известны. Одна из граней кубика параллельна стенке. Под каким углом `beta` кубик отскочит от стенки? Считайте, что перпендикулярная стенке составляющая скорости кубика в результате соударения не изменяется по величине.
Силы, действующие на кубик в процессе соударения, показаны на рис. 5.
По второму закону Ньютона
`Delta vec p = (m vec g + vecN_(«г») + vecF_(«тр») + vecN_(«в») ) * Delta t`.
Переходя к проекциям на горизонтальные оси `Ox` и `Oy`, получаем
Просуммируем приращения `Delta p_y = N_sf»в» Delta t` по всему времени `tau` соударения, получим:
Что такое импульс системы материальных точек
Найдём скорость `(Delta vec P_sf»с»)/(Delta t)` изменения импульса системы материальных точек (ответ на такой вопрос для одной материальной точки нам известен). Для примера рассмотрим систему двух материальных точек. Будем считать, что на первую материальную точку действуют суммарной силой `vec F_1` внешние по отношению к системе тела и внутренняя сила `vec f_(12)` со стороны второго тела. В свою очередь, на вторую материальную точку действуют внешние по отношению к системе тела, сумма этих сил `vec F_2` и внутренняя сила `vec f_(21)` со стороны первого тела. Тогда с учётом второго закона Ньютона для каждого тела получаем
`(Delta vec P_(«с»))/(Delta t) = (Delta vec p_1)/(Delta t) + (Delta vec p_2)/(Delta t) = (vec F_1 + vec f_(12)) + (vec F_2 + vec f_(21))`.
По третьему закону Ньютона `vec f_(12) + vec f_(21) = vec (0)`, и мы приходим к теореме об изменении импульса системы материальных точек:
`(Delta vec P_(«с»))/(Delta t) = vec F_1 + vec F_2`,
т. е. скорость изменения импульса системы материальных точек равна векторной сумме всех внешних сил, действующих на систему.
Из приведённого доказательства следует, что третий закон Ньютона можно сформулировать и как требование сохранения импульса системы взаимодействующих тел, если нет никаких других внешних сил.
Клин массой `M` находится на шероховатой горизонтальной поверхности стола. На клин положили брусок массой `m` и отпустили. Брусок стал соскальзывать, а клин остался в покое. Коэффициент трения скольжения бруска по поверхности клина равен `mu`, наклонная плоскость клина составляет с горизонтом угол `alpha`. Найдите горизонтальную `R_1` и вертикальную `R_2` силы (рис. 6), с которыми клин действует на опору.
Силы `vec F_(«тр»)` и `vecN_(«г»)`, наряду с силами тяжести, являются внешними по отношению к системе «клин + брусок» и определяют скорость изменения импульса этой системы.
Импульс `vecP_(«с»)` системы направлен по скорости бруска и по величине равен произведению массы бруска на его скорость `vecP_(«с») = vec p = m vec v (t)`. Для определения скорости изменения импульса `vec p` бруска обратимся ко второму закону Ньютона (рис. 8):
`(Delta vec p)/(Delta t) = m vec g + vec N + vecf_(«тр»)`.
Переходя к проекциям приращений импульса бруска и сил на оси `Oy` и `Ox` с учётом соотношения `f_sf»тр» = mu N` получаем:
По теореме об изменении импульса системы «клин + брусок»
`(Delta vec(P_sf»с»))/(Delta t) = M vec g + m vec g + vec N_(«г») + vecF_(«тр»)`.
Переходя в последнем равенстве к проекциям на горизонтальное и вертикальное направления (рис. 7), с учётом
Отсюда находим искомые силы
К этим же результатам можно прийти, анализируя движение на «традиционном языке» сил и ускорений с использованием формулы (2).
Физика. 10 класс
Импульс тела и импульс силы
Импульс. Закон сохранения импульса
Необходимо запомнить
Импульс тела равен сумме импульсов отдельных элементов.
Импульс системы тел равен векторной сумме импульсов каждого из тел системы:
Силы, с которыми взаимодействуют между собой тела системы, называют внутренними, а силы, создаваемые телами, не принадлежащими к данной системе, – внешними.
Систему, на которую не действуют внешние силы, или векторная сумма внешних сил равна нулю, называют замкнутой.
Абсолютно неупругий удар – столкновение тел, в результате которого они соединяются вместе и движутся дальше как одно целое.
Абсолютно упругий удар – столкновение тел, в результате которого не происходит соединения тел в одно целое и их внутренние энергии остаются неизменными.
Закон сохранения импульса:
Решение задачи на применение закона сохранения импульса
Количество движения
Французский учёный Рене Декарт попытался импульс использовать как величину, заменяющую силу. Потому что силу измерять достаточно сложно, а измерить массу и скорость несложно. Поэтому часто говорят, что импульс – это количество движения (именно Ньютон впервые назвал количеством движения произведение массы тела на скорость).
Декарт, судя по его высказываниям, понимал фундаментальное значение введенного им в XVII веке понятия количества движения – или импульса тела – как произведения массы тела на величину его скорости. И хотя он совершил ошибку, не рассматривая количество движения как векторную величину, сформулированный им закон сохранения количества движения выдержал с честью проверку временем. Ошибка была исправлена в начале XVIII века, и триумфальное шествие этого закона в науке и технике продолжается по сию пору.
. Декарт обосновывал принцип сохранения количества движения совершенством бога, «действующего с величайшим постоянством и неизменностью».
. закон сохранения импульса позволяет «разыскать» и невидимые объекты, например, электромагнитные волны, излучаемые открытым колебательным контуром, или антинейтрино – субатомные частицы, не оставляющие следов в детекторах.
Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено