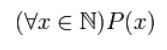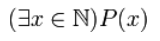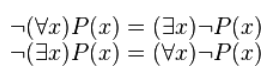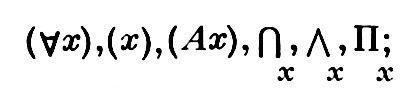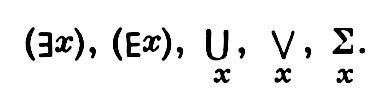что такое квантор в логике

Квантор

Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих выcказывание. Чаще всего упоминают:

В математической логике приписывание квантора к формуле называется связыванием или квантификацией.

В многозначных логиках также вводятся и другие кванторы, например, квантор плюральности (квантор Решера) (обозначается перевёрнутой M, читается «для большинства …»).

Содержание

Примеры

Обозначим предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные):

.

Следующие (уже истинные) высказывания используют квантор существования:

Их формальная запись:

.

Введение в понятие

Пусть на множестве простых чисел задан предикат : «Простое число нечётно». Подставим перед этим предикатом слово «любое». Получим ложное высказывание «любое простое число нечётно» (это высказывание ложно, так как 2 — простое чётное число).

Подставив перед данным предикатом слово «существует», получим истинное выcказывание «Существует простое число , являющееся нечётным» (например, ).

Таким образом, превратить предикат в высказывание можно, поставив перед предикатом слова («все», «существует» и другие), называемые в логике кванторами.

Кванторы в математической логике

(«При всех значениях (x) утверждение верно»).

(«Существует (x) при котором утверждение верно»).

Свободные и связанные переменные

Множество свободных переменных* формулы F определяется рекурсивно, следующим образом:

Связанное переименование, свободное переименование

Операции над кванторами

Правило отрицания кванторов — применяется для построения отрицаний высказываний, содержащих кванторы, и имеет вид:

История появления

Философы давно обращали внимание на логические операции, ограничивающие область истинности предиката, однако не выделяли их в отдельный класс операций. Так, Томас Гоббс считал, что они являются частями имен. [1]

Хотя кванторно-логические конструкции широко используются как в научной, так и в обыденной речи, их формализация произошла только в 1879 г., в книге Фреге «Исчисление понятий». Обозначения Фреге имели вид громоздких графических конструкций и не были приняты. Впоследствии было предложено множество более удачных символов, но общепринятыми стали обозначения для квантора существования (перевёрнутая первая буква англ. Exists — существует), предложенное Чарльзом Пирсом в 1885 г., и для квантора общности (англ. All — все), образованное Герхардом Генценом в 1935 г. по аналогии с символом квантора существования. Термины «квантор», «квантификация» также предложил Пирс.

Литература

Ссылки

Примечания

Полезное

Смотреть что такое «Квантор» в других словарях:

КВАНТОР — логический оператор, с помощью которого высказывание о к. л. отдельном объекте преобразуется в высказывание о совокупности (множестве) таких объектов. В логике используется два основных К.: К. общности, «V», и К. существования, «Э». В… … Философская энциклопедия

квантор — сущ., кол во синонимов: 1 • оператор (24) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

квантор — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN quantifier … Справочник технического переводчика

КВАНТОР — общее название для логических операций, к рые по предикату Р(х)строят высказывание, характеризующее область истинности предиката Р(х). В математич. логике наиболее употребительны квантор всеобщности и квантор существования Высказывание означает,… … Математическая энциклопедия

Квантор — (от лат. quantum сколько) символ, используемый для обозначения некоторых операций математической логики, одновременно логическая операция, дающая количественную характеристику области предметов, к которым относится выражение, получаемое в… … Начала современного естествознания

квантор — а, ч., лог. Логічний оператор, який переводить одну висловлювальну форму в іншу. Квантор існування … Український тлумачний словник

квантор — kvantorius statusas T sritis automatika atitikmenys: angl. quantifier vok. Quantor, m rus. квантор, m pranc. quantifier, m … Automatikos terminų žodynas

Квантор — (от лат. quantum сколько) логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа… … Большая советская энциклопедия

квантор — кв антор, а … Русский орфографический словарь

Источник

Предикаты и кванторы

Вы будете перенаправлены на Автор24

Понятие предиката

Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Примеры предикатов

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

Готовые работы на аналогичную тему

Операции над предикатами

Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.

Кванторы

Чаще всего используют кванторы:

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов

С помощью квантора всеобщности можно записать следующие ложные высказывания:

который будет иметь вид:

Для записи истинных высказываний используем квантор существования:

Запись будет иметь вид:

Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами

Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:

Источник

КВАНТОР

Полезное

Смотреть что такое «КВАНТОР» в других словарях:

квантор — сущ., кол во синонимов: 1 • оператор (24) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

квантор — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN quantifier … Справочник технического переводчика

КВАНТОР — общее название для логических операций, к рые по предикату Р(х)строят высказывание, характеризующее область истинности предиката Р(х). В математич. логике наиболее употребительны квантор всеобщности и квантор существования Высказывание означает,… … Математическая энциклопедия

Квантор — (от лат. quantum сколько) символ, используемый для обозначения некоторых операций математической логики, одновременно логическая операция, дающая количественную характеристику области предметов, к которым относится выражение, получаемое в… … Начала современного естествознания

квантор — а, ч., лог. Логічний оператор, який переводить одну висловлювальну форму в іншу. Квантор існування … Український тлумачний словник

квантор — kvantorius statusas T sritis automatika atitikmenys: angl. quantifier vok. Quantor, m rus. квантор, m pranc. quantifier, m … Automatikos terminų žodynas

Квантор — (от лат. quantum сколько) логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа… … Большая советская энциклопедия

квантор — кв антор, а … Русский орфографический словарь

Источник

MT1102: Линейная алгебра (введение в математику)

В алгебре высказываний применяют логические знаки для записи различных утверждений. Однако нам не достаточно этих знаков для выражения мысли типа «Всякий элемент %%x%% из множества %%D%% обладает свойством %%P(x)%%».

Понятие кванторов

Введем новые логические знаки, обозначаемые %%\forall%%, %%\exists%% и %%\exists!%%. Знак %%\forall%% называется квантором всеобщности, знак %%\exists%% — квантором существования, а %%\exists!%% — квантором существования и единственности.

Пусть %%P(x)%% — одноместный предикат, определенный на множестве %%D%%.

Квантор всеобщности

Используя квантор всеобщности, можно составить следующее высказывание

Читается как: «для любого %%x%% выполняется %%P(x)%%»; «для всякого %%x

P(x)%%»; «для всякого %%x%% верно %%P(x)%%» и т.п.

Пусть %%P(x)%% предикат %%x^2 \geq 0%%, определенный на множестве действительных чисел %%D = \mathbb R %%. Тогда высказывание %%\forall x

P(x)%% имеет вид %%\forall x

x^2 \geq 0%%. Это истинное высказывание, так как для любого значения пременной %%x = a \in \mathbb R %% получаем истинное высказывание %%a^2 \geq 0%%. Однако, высказывание %%\forall x

x^2 > 0%% ложно, например, как при %%x = 0%% получаем ложное высказывание %%0 > 0%%.

Квантор существования

Используя квантор существования, можно составить следующее высказывание

Читается как: «существует %%x%% такой, что %%P(x)%%»; «существует %%x%% с условием %%P(x)%%» и т.п.

Квантор существования и единственности

Используя квантор существования и единственности, можно составить следующее высказывание

Читается как: «существует единственный %%x%% такой, что %%P(x)%%»; «существует единственный %%x%% с условием %%P(x)%%» и т.п.

Отрицание «кванторов»

Докажем первое из них. Пусть высказываине %%\overline<\forall x

P(x)>%% истинно. Тогда высказывание %%\forall x

P(x)%% ложно. Поэтому для некоторого %%x = a%% имеем %%P(a)%% ложно. Тогда %%\overline%% истинно. Итак, для некоторого значения %%x = a

\overline%% истинно. Поэтому высказывание %%\exists x

Аналогично доказывается второе утверждение.

Применение одного из кванторов «понижает» степень предиката на единицу. Из двуместного предиката получается одноместный предикат, а из одноместного — предикат %%0%% степени или высказывание.

Правила перестановки кванторов

P(x,y) \equiv \exists y

P(x,y) \equiv \forall y

Однако, разноименные кванторы переставлять местами нельзя. Рассмотрим двуместный предикат %%P(x, y): x + y = 0%%, определенный на множестве %%\mathbb R%%. Тогда высказывание %%\exists x

x + y = 0%% можно прочитать так: «существует %%x%%, которое в сумме с любым %%y%% равно 0». Это ложно высказывание.

Переставим разноименные кванторы местами и получим высказывание %%\forall y

x+ y = 0%%, которое можно прочитать так: «для любого %%y%% существует %%x%% такой, что их сумма равна 0». Это истинное высказывание. В итоге получили различные истинностные значения высказываний.

Для записи одноименных кванторов существуют следующие сокращения:

\forall y \equiv \forall x, y

\exists y \equiv \exists x, y. \end $$

Источник

Кванторы

Наивное определение кванторов

Определить истинность или ложность подобных выражений при помощи таблиц истинности проблематично.

Когда кванторы не пререстановочны

Различные кванторы не перестановочны: «для любого \(x\) существует \(y\)» не тоже, что «некий \(y\) существует для любого \(x\)»: \[ \forall_x \, \exists_y\, A(x,y)

\exists_y\, \forall_x \, A(x,y). \] В обыденной жизни подобная неэквивалентность вполне естественна. Пусть \(A(x,y)\): «\(x\) имеет мать \(y\)». Тогда очевидно, что для «любого \(x\) существует мать \(y\)», тогда как утверждение «некая \(y\) является матерью всех людей \(x\)» истинно только в очень специфическом мире. Чтобы доказать не общезначимость формулы (т.е. что она не тавтология) достаточно придумать пример где она ложна.

\(\diamond\) Пусть предметная область — это натуральные числа: \(0,1. \), а предикат \(A(x,y):

Однотипные кванторы пререстановочны

Однотипные кванторы, можно переставлять местами: \[ \begin \forall_x\,\forall_y\,A(x,y) &

& \exists_y\,\exists_x\,A(x,y). \end \] В таких формулах иногда будет использоваться сокращение \(\forall_:

\forall_x\forall_y\) и аналогично для \(\exists\). Таким образом \(\forall_\equiv \forall_\) и \(\exists_\equiv \exists_\). Число аргументов предикатов, входящих в формулу, произвольно. Например, справедливо: \(\forall_x\,\forall_y\,A(w,x,v,y,z)

Другие свойства кванторов

Отрицание можно «проносить» через квантор, меняя его: \[ \begin \neg \forall_x\, A(x) &

& \exists_x\, \neg A(x),\\[2mm] \neg \exists_x\, A(x) &

& \forall_x\, \neg A(x). \end \] («если не верно для всех \(x\), то есть \(x\) для которого ложно»).

Действие любого квантора (\(\mathcal=\exists

\forall\)) можно расширять, вынося за дизъюнкцию или конъюнкцию (правила расширения действия): \[ \begin \mathcal_x\, A(x)

& \mathcal_x\, \bigr(A(x) \,\&\, B\bigr),\\[2mm] \mathcal_x\, A(x) \,\vee\, B &

& \mathcal_x\, \bigr(A(x) \vee B\bigr), \end \] где отсутствие явного указания у предиката \(B\) аргумента \(x\) означает, что он от \(x\) не зависит, а при отсутствии скобок приоритет кванторов считается максимальным, т.е. \(\forall_x A(x)\,\&\. \) — это \((\forall_x A(x))\,\&\. \) и т.д.

Наконец, для родственных операций (\(\&\) для \(\forall\) и \(\vee\) для \(\exists\) ) можно объединять кванторы ( правила объединения): \[ \begin \forall_x\,\forall_y\, \bigr(A(x)\,\&\,B(y)\bigr) &

& \forall_x\, \bigr(A(x)\,\&\,B(x)\bigr),\\[2mm] \exists_x\,\exists_y\, \bigr(A(x)\vee B(y)\bigr) &

& \exists_x\, \bigr(A(x)\vee B(x)\bigr). \end \]

Полезны также тождества разбиения: \[ \begin \forall_x\,\forall_y\, A(x,y) &

\forall_x\forall_y\,\bigr(x\neq y \,\to\,A(x,y)\bigr),\\[2mm] \exists_x\,\exists_y\, A(x,y) &

Для конечных предметных областей все эти тождества несложно доказать при помощи алгебры логики, записав квантор всеобщности как цепочку логических И, а квантор существования как цепочку логических ИЛИ. Постулируется, что все эти тождества справедливы не только для конечных, но и для бесконечных множеств.

Доказательства

Перестановочность кванторов непосредственно следует из коммутативности \(A\,\&\,B\equiv B\,\&\,A\) и правил поглощения \(A\,\&\,A\equiv A\).

Тождества с отрицанием следуют из правил \(\neg(A\,\&\, B)

\neg A\vee \neg B\): \[ \neg \forall_x\, A(x)

\exists_x\, \neg A(x), \] где \(A_i=A(x_i)\). Также легко доказываются правила расширения для родственных операций. Например \(\forall_x\, A(x) \,\&\, B

\forall_x\, \bigr(A(x) \,\&\, B\bigr)\) это \[ (A_1\,\&\,A_2\,\&\. )\,\&\,B \equiv (A_1\,\&\,B)\,\&\,(A_2\,\&\,B)\,\&\. \] где учтена ассоциативность, коммутативность и поглощение \(B\,\&\,B\equiv B\). Для неродственных операций используется свойство дистрибутивности. Так \(\forall_x\, A(x) \vee B

\forall_x\, \bigr(A(x) \vee B\bigr)\) это \[ (A_1\,\&\,A_2\,\&\. )\vee B \equiv (A_1\vee B)\,\&\,(A_2\vee B)\,\&\. \] Чтобы обосновать правила объединения кванторов с родственными операциями, распишем в \(\forall_x\forall_y\, \bigr(A(x) \,\&\, B(y))\) сначала \(\forall_y\), а затем \(\forall_x\): \[ (A_1\&\,B_1)\,\&\,(A_1\&\,B_2)\,\&\,(A_1\&\,B_3)\,\&\. (A_2\,\&\,B_1)\,\&\,(A_2\&\,B_2)\,\&\,(A_2\,\&\,B_3)\,\&\. \] По свойству поглощения это: \((A_1\,\&\,B_1)\,\&\,(A_2\,\&\,B_2)\,\&\. \equiv \forall_x\,(A_x\,\&\,B_x)\). Аналогично доказываются тождества разбиения.

Число существований

Пусть в теории определён предикат равенства \(x=y\), позволяющий выяснять одинаковы ли две сущности \(x\) и \(y\). С его помощью можно детализировать количество существующих объектов. Например:

Не более одного объекта \(\<0,1\>\) обладает свойством \(A\): \[ \forall_\, [ A(x)\,\&\,A(y) \to x=y ]. \]

Один и только один объект \(\<1\>\) обладает свойством \(A\): \[ \exists_x\,A(x)

\forall_\, [ A(x)\,\&\,A(y) \to x=y ]. \] Последний вид существования в единственном экземпляре иногда обозначают при помощи квантора с восклицательным знаком: \(\exists^_\,A(x)\). Аналогично строятся формулы относительно двух сущностей:

По меньшей мере два объекта \( \<2,3. \>\) обладают свойством \(A\): \[ \exists_\, [ A(x)\,\&\,A(y) \,\&\, x\neq y ]. \]

Не более двух объектов \(\<0,1,2\>\) обладают свойством \(A\): \[ \forall_\, [ A(x)\,\&\,A(y)\,\&\,A(z)

y=z) ]. \] Объединение двух последних формул логическим «И» приведёт к фразе: «в точности два объекта обладают свойством \(A\)». Подобным образом можно говорить о трёх сущностях, и т.д.

Источник