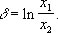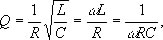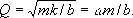что такое логарифмический декремент затухания
Что такое логарифмический декремент затухания
3) Свободные затухающие колебания. Декремент и логарифмический декремент затухания. Добротность колебательной системы.
Свободные затухающие колебания.
Декремент и логарифмический декремент затухания.
Декремент затухания, количественная характеристика быстроты затухания колебаний. Д. з. d равен натуральному логарифму отношения двух последующих максимальных отклонений х колеблющейся величины в одну и ту же сторону:
Д. з. — величина, обратная числу колебаний, по истечении которых амплитуда убывает в е раз. Например, если d = 0,01, то амплитуда уменьшится в е раз после 100 колебаний. Д. з. характеризует число периодов, в течение которых происходит затухание колебаний, а не время такого затухания. Полное время затухания определяется отношением Т/d.
Добротность колебательной системы.
Добротность колебательной системы, отношение энергии, запасённой в колебательной системе, к энергии, теряемой системой за один период колебания. Добротность характеризует качество колебательной системы, т.к. чем больше Д. к. с., тем меньше потери энергии в системе за одно колебание. Д. к. с. Q связана с логарифмическим декрементом затухания d; при малых декрементах затухания Q » p/d. В колебательном контуре с индуктивностью L, ёмкостью C и омическим сопротивлением R Д. к. с.
где w — собственная частота контура. В механической системе с массой m, жёсткостью k и коэффициентом трения b Д. к. с.
Добротность — количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний при резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты. На этом свойстве основан метод измерения Д. к. с. Величина добротности характеризует также и избирательность колебательной системы; чем больше добротность, тем уже полоса частот внешней силы, которая может вызвать интенсивные колебания системы. Экспериментально Д. к. с. обычно находят как отношение частоты собственных колебаний к полосе пропускания системы, т. е. Q = w/Dw. Численные значения Д. к. с.: для радиочастотного колебательного контура 30—100; для камертона 10000; для пластинки пьезокварца 100000; для объёмного резонатора СВЧ колебаний 100—100000.
Что такое логарифмический декремент затухания
Чему равен логарифмический декремент затухания?
Савельев И.В, т.1, стр. 206
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно
Это отношение называют дектрементом затухания,
а его логарифм – логарифмическим декрементом затухания:
(58.9)
Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
называется декрементом затухания, а его логарифм
(146.7)
— логарифмическим декрементом затухания; Ne — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.
Логарифмический декремент колебаний
Логарифмический декремент колебаний — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины в одну и ту же сторону:
Логарифмический декремент колебаний равен декременту, умноженному на период колебаний:
Полезное
Смотреть что такое «Логарифмический декремент колебаний» в других словарях:
логарифмический декремент колебаний — логарифмический декремент Ндп. логарифмический декремент затухания Натуральный логарифм отношения двух последовательных максимальных или минимальных значений величины при затухающих свободных колебаниях. Пояснения 1)Некоторые величины и… … Справочник технического переводчика
Логарифмический декремент колебаний — 107. Логарифмический декремент колебаний Логарифмический декремент Ндп. Логарифмический декремент затухания Натуральный логарифм отношения двух последовательных максимальных или минимальных значений величины при затухающих свободных колебаниях… … Словарь-справочник терминов нормативно-технической документации
Логарифмический декремент затухания — D Величина, показывающая скорость затухания собственных колебаний и определяемая как натуральный логарифм отношения следующих друг за другом амплитуд колебаний Источник … Словарь-справочник терминов нормативно-технической документации
логарифмический декремент — logarithmic decrement Натуральный логарифм отношения двух любых последовательных одинакового знака максимальных амплитуд при затухании одночастотных колебаний. Шифр IFToMM: 3.9.38 Раздел: КОЛЕБАНИЯ В МЕХАНИЗМАХ … Теория механизмов и машин
ДЕКРЕМЕНТ ЗАТУХАНИЯ — (от лат. decrementum уменьшение, убыль), количественная хар ка быстроты затухания колебаний. Д. з. d равен натуральному логарифму отношения двух последующих макс. отклонений х колеблющейся величины в одну и ту же сторону: d=ln(x1/x2). Д. з.… … Физическая энциклопедия
ДЕКРЕМЕНТ ЗАТУХАНИЯ — логарифмический (от лат. decrementum уменьшениеубыль) количеств. хар ка затухания колебаний в линейной системе. Д. з. равен натур. логарифму отношения двух последовательных Макс. отклонений колеблющейся величины в одну и ту же сторону … Большой энциклопедический политехнический словарь
Затухание колебаний — характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто носит колебательный характер … Энциклопедия техники
затухание колебаний — затухание колебаний характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто… … Энциклопедия «Авиация»
затухание колебаний — затухание колебаний характеристика возмущенного движения летательного аппарата. Движение летательного аппарата развивающееся после отклонения от исходного режима полёта под действием внешних возмущений или управляющих воздействий, часто… … Энциклопедия «Авиация»
Затухание колебаний — уменьшение интенсивности колебаний с течением времени, обусловленное потерей энергии колебательной системой. Простейшим случаем убыли энергии колебания является превращение её в тепло вследствие трения в механических системах и… … Большая советская энциклопедия
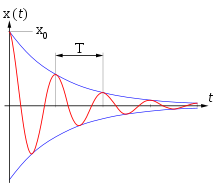
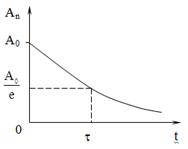
Период затухающих колебаний
.
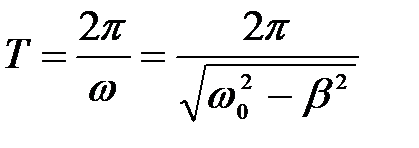
Логарифмический декремент затухания d характеризует быстроту затухания колебаний
,
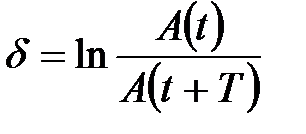
где A(t) и A(t+T) – амплитуды двух соседних колебаний.
Для N полных колебаний
.
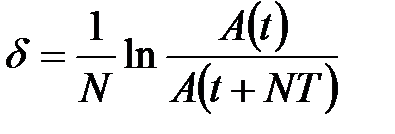
Найдем связь между логарифмическим декрементом затухания и коэффициентом затухания
.
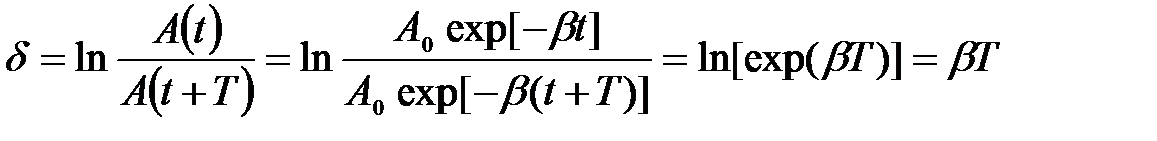
Выясним физический смысл коэффициента затухания. Обозначим через t время, в течение которого амплитуда колебаний уменьшается в е = 2,718 раз. Тогда
,
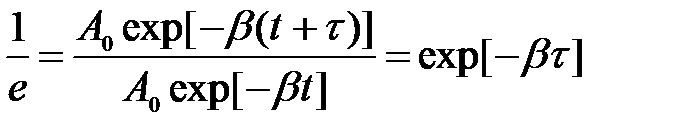
следовательно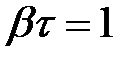 
.
Физический смысл коэффициента затухания b. Коэффициент затухания есть величина, обратная времени, за которое амплитуда колебаний уменьшается в e раз
.
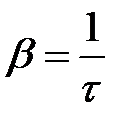
Выясним физический смысл логарифмического декремента затухания.
,
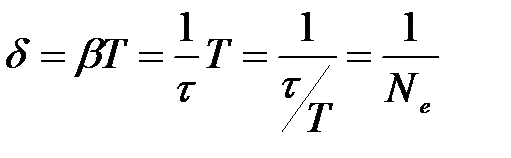
где Ne – число колебаний, происходящих за время t.
Физический смысл логарифмического декремента затухания d.
Логарифмический декремент затухания есть величина, обратная числу колебаний Ne, по завершению которых амплитуда уменьшается в е = 2,718 раз
.
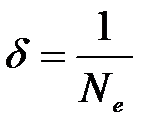
Добротность (см. Приложение II. п.2)
Логарифмический декремент затухания и добротность колебательной системы
Для количественной характеристики затухания, кроме коэффициента затухания d, используют логарифмический декремент затухания. Введение последнего обосновано тем, что отношение двух любых последовательных амплитуд Аn и Аn+1 остается постоянным в течение всего процесса, т. е.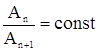 
.
Логарифмический декремент равен натуральному логарифму отношения двух последовательных амплитуд:
.
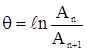
Декремент – число (безразмерная величина), характеризующее быстроту затухания колебаний во времени. Выразим Аn и An+1 :
,
.
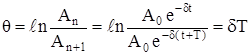
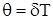
Логарифмический декремент прямо пропорционален коэффициенту затухания d. Если затухания в системе нет: d = 0, то и q = 0.
Физический смысл декремента: величина, обратная декременту (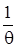
), равна числу колебаний n, через которое амплитуда колебаний уменьшается в е раз.
Для характеристики затухания используется и время релаксации t, за которое амплитуда уменьшается в е раз.
.
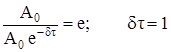
Получаем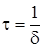 
, т. е. время релаксации обратно пропорционально коэффициенту затухания.
Качество колебательной системы определяется ее добротностью. Чем медленнее рассеивается энергия, тем добротнее система. Добротность определяется соотношением
,
где Е(t) – полная энергия колебательной системы в момент времени t; Е(t + T) – энергия в момент времени t + T т. е. спустя период; Е(t) – E(t + T) – энергия, рассеянная за период.
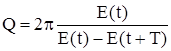
Так как полная энергия пропорциональна квадрату амплитуды колебания Е
. Добротность будет равна:
.
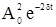
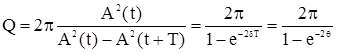
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет