что такое модельное время
3. Модельное время
Имитационное моделирование, как правило, проводится с использованием средств вычислительной техники в соответствии с программой, реализующей последовательность возникающих в системе основных событий, т.е. соответствующий процесс функционирования системы. При этом несколько часов, суток, лет работы реальной системы моделируется за несколько секунд, минут, часов работы компьютера.
При имитационном моделировании различают три вида времени.
1. Время реальной системы — это время, в котором «живет», функционирует моделируемая система.
2. Модельное время — это «искусственное» время, в котором «живет» модель или другими словами это время, которое является имитацией, прообразом (моделью) времени реальной системы.
3. Реальное время — это время, в котором живет исследователь, компьютер или другими словами это время необходимое для моделирования (затратное время).
Для нас наибольший интерес представляет модельное время. Для того, чтобы вести отсчет модельного времени и обеспечить правильную хронологическую последовательность наступления основных событий в имитационной модели используется так называемый таймер модельного времени, которая представляет собой переменную для хранения (фиксации) текущего значения модельного времени.
В процессе моделирования системы, таймер модельного времени, безусловно, должен постоянно корректироваться в соответствии с теми основными событиями, которые возникают в реальной системе. При этом существуют два способа (два принципа) коррекции значения таймера модельного времени:
1) коррекция с постоянным шагом (принцип t);
2) коррекция с переменным шагом (принцип z).
В первом случае при каждой коррекции модельное время увеличивается на одно и то же значение t, выбираемое перед началом моделирования, а во втором случае значение приращения таймера каждый раз является случайной, а, значит, переменной величиной.
Р
В модели, где время корректируется с постоянным шагом по принципу t(рис.3.1, б) модельное времяtMбудет последовательно принимать значенияt1‘=t, t2‘=2t,t3‘=3tи т.д. Эти моменты модельного времени никак не связаны с моментамиt1,t2,t3. появления событий в реальной системе. При этом подходе после очередного приращения таймера на величинуtпроверяется, не произошли ли на этом интервале в системе какие-нибудь события. Если есть такие события, то они обрабатываются, считая, что они якобы произошли в текущий момент модельного времени (правая граница интервала приращения), хотя реально события появились в другие моменты времени из интервалаt. Очевидно, что при этом обработка событий может производиться группами. Выбор значенияtоказывает существенное влияние на результаты моделирования с точки зрения адекватности отражения реальных событий в модели и затрат ресурсов компьютера на моделирование. Еслиtзадать большим, то результаты моделирования могут быть недостоверными, т.к. все большее число событий группируется и обрабатывается в одной точке модельного времени. С другой стороны, уменьшениеtдля того, чтобы два неодновременных события не попали в один и тот же интервалt, а, следовательно, обрабатывались в разные моменты модельного времени, приводит к увеличению затрат на моделирование, т.к. значительная часть ресурсов будет тратиться на коррекцию таймера и на отслеживание событий, которых в большинстве интерваловtпри этом могут и не быть. При любом уменьшенииt всегда остается возможность попадания двух неодновременных событий в один и тот же временной интервалt.
В модели, где время корректируется с переменным шагом или по принципу z, значения, принимаемые модельным временем, совпадают, а значит, непосредственно связаны с моментами возникновения событий в реальной системе:t1«=t1,t2«=t2,t3«=t3. Достигается это тем, что при очередном приращении (после отработки события в текущий момент времени) модельное время сдвигается вперед до момента наступления следующего (ближайшего по времени) события. Отсюда, каждый раз модельное время получает переменное приращение, равное интервалу между двумя последовательными основными событиями. Очевидно, что при таком подходе, события отрабатываются в той последовательности, в те моменты времени, в которые они возникают в реальной системе. При этом одновременная обработка событий в модели имеет место только тогда, когда эти события появляются одновременно и в реальной системе (событияС5иС6на рис.3.1).
При любом способе коррекции таймера модельного времени, в начале моделирования, таймер, как правило, устанавливается на нулевое значение (tM =0). При этом разработчик сам решает вопрос о том, какое значение времени реальной системы принять за точку нулевого отсчета. Например, если необходимо моделировать процесс функционирования некоторой системы в течение суток, то началу отсчета модельного времени может соответствовать 8 часов утра, 12 часов дня и т.д. Кроме того, разработчик самостоятельно решает и вопрос о выборе единицы модельного времени и все значения времени, входящие в модель или получаемые при моделировании, должны быть выражены через выбранную единицу.
Еще один вопрос, который надо решить в начале моделирования, это условие (или условия) завершения моделирования. В общем случае, в качестве такого условия можно принять некоторое условие, которое может иметь место в моделируемой системе. В ходе моделирования модель проверяет возникновение соответствующего условия в системе и как только это условие возникает, модель принимает решение об окончании моделирования.
Однако, на практике, как правило, поступают гораздо проще, а именно, в начале моделирования задается время моделирования Ти по достижению модельным временем этого значения, т.е. когдаtM Т,принимается решение о завершении моделирования и модель переходит к обработке полученных результатов. Иногда это условие дополняется другими условиями завершения моделирования. Например, дополнительным условием может быть условие дообслуживания тех заявок, которые оказались в СМО в момент времениtM=Т.
Для реализации способа завершения моделирования по выполнению условия tMТс тем, чтобы при каждой коррекции таймера не проверять выполнение этого условия, в модель можно ввести основное псевдо-событие «окончание моделирования». Такое событие укладывается в концепцию основных событий как событий, которых можно планировать заранее, т.к. момент наступления события «окончание моделирования» задается заранее в начале моделирования.
На рис. 3.1. введенное псевдо-событие обозначено через С0 с моментом наступленияТ.Если после очередной коррекции модельного времени выяснится, что наступило событие «окончания моделирования», то принимается соответствующее решение.
Далее в качестве способа коррекции таймера модельного времени будем использовать способ коррекции с переменным шагом в силу очевидных достоинств, присущих данному способу.
Понятие о модельном времени. Механизм продвижения модельного времени. Дискретные и непрерывные имитационные модели



Для описания динамики моделируемых процессов в имитационном моделировании реализован механизм задания модельного времени. Эти механизмы встроены в управляющие программы любой системы моделирования.
Если бы на ЭВМ имитировалось поведение одной компоненты системы, то выполнение действий в имитационной модели можно было бы осуществить последовательно, по пересчету временной координаты. Чтобы обеспечить имитацию параллельных событий реальной системы вводят некоторую глобальную переменную (обеспечивающую синхронизацию всех событий в системе) t0, которую называют модельным (или системным) временем.
Существуют два основных способа изменения t0:
В случае пошагового метода продвижение времени происходит с минимально возможной постоянной длиной шага (принцип t). Эти алгоритмы не очень эффективны с точки зрения использования машинного времени на их реализацию.
По-событийный метод (принцип «особых состояний»). В нем координаты времени меняются только когда изменяется состояние системы. В по-событийных методах длина шага временного сдвига максимально возможная. Модельное время с текущего момента изменяется до ближайшего момента наступления следующего события. Применение по-событийного метода предпочтительно в случае, если частота наступления событий невелика, тогда большая длина шага позволит ускорить ход модельного времени. На практике по-событийный метод получил наибольшее распространение.
Способ фиксированного шага применяется:
если закон изменения от времени описывается интегро-дифференциальными уравнениями. Характерный пример: решение интегро-дифференциальных уравнений численным методом. В подобных методах шаг моделирования равен шагу интегрирования. При их использовании динамика модели является дискретным приближением реальных непрерывных процессов; когда события распределены равномерно и можно подобрать шаг изменения временной координаты; когда сложно предсказать появление определенных событий; когда событий очень много и они появляются группами.
В остальных случаях применяется по-событийный метод. Он предпочтителен, когда события распределены неравномерно на временной оси и появляются через значительные временные интервалы.
Таким образом, вследствие последовательного характера обработки информации в ЭВМ, параллельные процессы, происходящие в модели, преобразуются с помощью рассмотренного механизма в последовательные. Такой способ представления носит название квазипараллельного процесса.
Простейшая классификация на основные виды имитационных моделей связана с применением двух этих способов продвижения модельного времени. Различают имитационные модели:
В непрерывных имитационных моделях переменные изменяются непрерывно, состояние моделируемой системы меняется как непрерывная функция времени, и, как правило, это изменение описывается системами дифференциальных уравнений. Соответственно продвижение модельного времени зависит от численных методов решения дифференциальных уравнений.
В дискретных имитационных моделях переменные изменяются дискретно в определенные моменты имитационного времени (наступления событий). Динамика дискретных моделей представляет собой процесс перехода от момента наступления очередного события к моменту наступления следующего события.
Поскольку в реальных системах непрерывные и дискретные процессы часто невозможно разделить, были разработаны непрерывно-дискретные модели, в которых совмещаются механизмы продвижения времени, характерные для этих двух процессов.
Модельное время и виды процессов
Ключевые слова: модельное время, процесс, дискретный (прерывный) процесс, аналоговый (непрерывный) процесс, шаг моделирования, диапазон (интервал моделирования, просчёт модели, аппроксимация, предобработка)
Просчёт любой модели предполагает обработку данных во времени. Следовательно, в выражении (1) присутствует время, которое выражено через изменение значений вектора параметров X. Это позволяет рассматривать все параметры системы в динамике. Но соответствует ли модельное время тому времени, которое рассматривается в физике? Практика показывает, что это происходит далеко не всегда, поэтому обратимся к определению.
& Модельное время (англ. model time) – критерий моделируемого объекта, имеющий однонаправленную динамику (возрастание или снижение), относительно изменения которого оцениваются остальные показатели исследуемой модели.
В качестве модельного времени показатель физического времени необязателен: динамику модели можно отслеживать относительно изменения любого удовлетворяющего определению показателя. Например, шкалой модельного времени может являться ценовой диапазон, для исследования поведения модели в котором последовательно рассчитываются другие критерии.
Таким образом, модельное время следует отличать от реального времени – исторической шкалы моделируемого объекта. Ещё одним понятием является машинное время, отражающее период времени, затрачиваемый ЭВМ на один полный просчёт модели.
Теперь следует рассмотреть свойства, которыми характеризуется модельное время. Рационально выделить четыре основные характеристики: это шкала моделирования (масштаб), шаг моделирования, диапазон моделирования и вид модельного времени. Рассмотрим их подробнее.
Шкала моделирования определяется той величиной, которая была взята в качестве базовой, то есть в качестве модельного времени. От этого зависит масштаб рассмотрения процессов, моделируемых в системе. Следовательно, от детализации, то есть от минимального деления шкалы времени моделирования, будет зависеть, в каких единицах измерения будут заданы шаг и диапазон моделирования.
Важным элементом модели является такой параметр, как шаг моделирования.
& Шаг моделирования (англ. step of calculation model) – совокупность действий, происходящих в единицу модельного времени и характеризующие очередной этап просчёта модели.
От того, какой длины будет выбран шаг моделирования, будет зависеть детальность и частота просчёта модели. Например, если моделируется значение курса акции предприятия на бирже с интервалом в 1 час, то можно получить довольно гладкую кривую, описывающую колебание её курса. Если же в качестве шага выбрать одну минуту, то можно получить сложную динамику, ярко демонстрирующую вклад случайных процессов (шумов) на результаты работы модели. Традиционно шаг моделирования выбирается константой, хотя существуют модели, в которых это правило сознательно нарушается. В данном пособии шаг моделирования везде будет считаться постоянным.
Для просчёта модели мало определить то, с какой частотой будет вестись прогон. Для корректного описания ситуации требуется знать интервал моделирования.
& Диапазон (интервал) моделирования (англ. interval of calculation model) – интервал шкалы модельного времени, на котором будет просчитана модель с частотой, равной шагу моделирования.
Очевидно, что диапазон моделирования можно задать двумя способами: первый – указать начальное и конечное значения на шкале модельного времени (например, работа завода в течение смены, то есть с 8:00 до 17:00, с учётом обеденного перерыва); и второе – отметить начальное значении, а затем указать длительность моделирования в терминах шкалы моделирования (например, начиная с 8:00 и далее 8 часов).
Рассмотрев модельное время, следует обратиться к вопросу описания процессов в моделях. Любые процессы в моделируемой системе относительно модельного времени можно разделить на два типа: аналоговые и дискретные. Дадим их определения:
& Аналоговый процесс (англ. analog process) – процесс, регистрируемый в виде непрерывного потока значений, постепенно переходящих от одного значения к другому.
& Дискретный процесс (англ. discreed process) – процесс, регистрируемый в виде последовательности отдельных значений, не позволяющих сделать однозначное заключение о характере перехода между соседними значениями.
Если известны все взаимодействия частей системы в виде формальных законов (обычно это уравнения), то модель строится на основе аналоговых процессов, имеющих непрерывную природу. Примером таких процессов могут быть значения, отражающие динамику высоты полёта метеозонда, температуры котла с расплавом стали, рыночного спроса на холодильники и пр. Аналоговые процессы изображаются непрерывной кривой или последовательностью точек, которые можно соединить отрезками (интерполировать) или огибающей кривой (аппроксимировать). Пример представлен на рис. 3, а. Запись аналоговой закономерности в виде уравнений называется аналитическим представлением.
 | |
| а | б |
Рис. 3. Пример изображения аналогового и дискретного процессов
В других ситуациях, когда нет исчерпывающей информации о моделируемом объекте, известны отдельные ряды значений интересующих исследователя показателей. Формул ещё нет, и поэтому значения представлены в виде последовательности точек, то есть как дискретный процесс. Например, временные ряды замечательно отражают динамику цен на товар в супермаркете, режимы работы оборудования в цехе, статистику операций на бирже и пр. Дискретные процессы изображаются в виде последовательности точек либо как гистограмма или ступенчатый график (рис. 3, б): в их значениях отражены отдельные состояния моделируемого процесса, переходы между которыми скачкообразны. Запись дискретной закономерности в виде временного ряда ещё называется эмпирическим представлением.
Просчёт модели в среде моделирования осуществляется равномерными шагами (квантуется). При этом нет разницы, задаются процессы в модели аналоговым законом (гладкой кривой) или дискретным (ломаная ступенчатая линия). Очевидно, что при ширине шага моделирования, стремящейся к нулю, динамика системы будет носить плавный, подробный, постепенный характер, а при значительной ширине – разрозненные, скачкообразные значения. Исходя из данной закономерности, всегда можно перейти от дискретного процесса к аналоговому и наоборот. Для получения отдельных значений процесса, описываемого дифференциальным законом, достаточно подставить в его уравнение значения модельного времени.
Из этого можно сделать вывод: важен не тип процессов, используемый в модели, а умение с ним правильно обращаться. Тогда возникает вопрос: при каких обстоятельствах рационально использовать тот или иной тип описания процесса? Выбор типа представления динамики процесса зависит от конкретной задачи и исходных данных. Каждый из них обладает как положительными, так и отрицательными чертами (табл. 1). Поэтому там, где не требуется результат повышенной точности, рационально переходить от одного типа к другому и обратно в соответствии с потребностями задачи и удобством работы.
В процессе работы с моделью нередко возникает такая ситуация, что отдельные ряды данных не могут быть корректно использованы для просчёта модели. Это связано с тем, что интервалы между значениями ряда могут быть неравномерны или иметь частоту, не совпадающую с шагом моделирования.
Например, концентрацию потока вещества ( 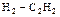
Характеристика типов процессов
| Тип процесса | Достоинства | Недостатки |
| Аналитическое представление (уравнение) | – детальное отражение динамики; – получение значений в любой точке; – быстрая реакция системы на управляющий сигнал | – необходимость учёта всех влияющих факторов; – требуются большие вычислительные мощности |
| Эмпирическое представление (дискретные данные) | – выявляют скрытые закономерности между разрозненными показателями; уточнение теории | – не выявляют быстрых изменений параметров; – точность зависит от объёма данных |
& Предобработка (англ. preprocessing) – процесс изменения исходных данных таким образом, чтобы они соответствовали условиям моделирования, существенно не искажая их значений и соотношения.
Иногда для этого процесса применяются термины пересчёт или нормализация данных[3]. Если рассматривать аналоговый по природе процесс (а в приведённом примере именно такой), то данные следует привести к значениям модельного времени. Для этого требуется осуществить ряд шагов:
1) описать в окрестностях исходных точек временного ряда гладкую кривую, наиболее адекватно отражающую исходную динамику (аппроксимировать);
2) найти уравнение получившейся кривой (полинома);
3) оценить степень погрешности (среднеквадратичное отклонение);
4) найти значения полинома в точках, соответствующих модельному времени.
При оценке адекватности аппроксимирующего закона следует руководствоваться тремя критериями:
1) коэффициент аппроксимации (среднеквадратичное отклонение) не должен превышать 0,95 (то есть он должен стремиться к единице);
2) степень полинома должна быть по возможности меньше;
3) аппроксимирующая кривая визуально должна довольно точно повторять динамику исходного ряда.
Новый ряд данных, после корректной нормализации, будет соответствовать условиям моделирования и может быть использован для просчёта в модели. Несмотря на некоторую потерю точности, это позволяет приводить данные к приемлемому для моделирования виду.
Ещё одним базовым термином, который важен при рассмотрении принципов процесса компьютерного моделирования, является термин событие.
& Событие (англ. event) – переход модели или её части в элементарное состояние, необходимое для фиксации моделируемых процессов, запуска какой-либо подпрограммы или остановки процесса просчёта модели (запланированно или в результате ошибки).
Оно позволяет проектировать процесс моделирования не только за счёт итерационного просчёта значений, но и в соответствии с некоторыми режимами её работы.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Модельное время
Необходимость представления параллельных по времени процессов в виде последовательного алгоритма приводит к введению глобальной переменной Т, называемой (системным) модельным временем. Существует еще две причины, по которым необходимо введение модельного времени.
1. Процессы в имитационной модели идут со скоростью, отличной от скорости их реализации в реальной системе. Модельное время используется для изменения масштаба времени исследуемой системы.
2. Программа для ЭВМ должна оперировать с конечным множеством данных, и, следовательно, имитировать поведение системы не во все моменты времени, а лишь в некоторые, составляющие конечное множество.
При разработке ИМ и планировании эксперимента следует соотносить между собой три представления времени: реальное, модельное время и машинное время, отражающее затраты времени на ЭВМ для проведения имитации.
Существуют два способа формирования конечного множества моментов модельного времени.
Первый способ – изменение модельного времени с постоянным шагом. При имитации первым способом интервал времени моделирования разбивается на интервалы фиксированной длины Dt. Затем на каждом интервале последовательно обрабатываются алгоритмы, имитирующие компоненты моделируемой системы, после чего происходит изменение модельного времени.
Для реализации принципа фиксированных интервалов математическая модель имитируемой системы должна быть предварительно преобразована к виду, допускающему рекуррентные вычисления.
Точность моделирования достигается ценой больших затрат машинного времени, находящихся в обратно пропорциональной зависимости от величины Dt. Обычно принцип фиксированных интервалов используется при построении моделей непрерывных динамических систем, описываемых системами дифференциальных уравнений различных типов. (Метод Эйлера)
В других случаях принцип Dt целесообразно использовать, если:
· события появляются регулярно и распределены равномерно на всем интервале моделирования и исследователь может подобрать интервал изменения Dt, обеспечивающий минимальную погрешность имитации;
· событий очень много и они появляются группами;
· невозможно заранее определить моменты появления событий.
Второй способ – моделирование по особым состояниям. При рассмотрении некоторых сложных систем можно обнаружить существенную неравноправность состояний системы в заданном интервале времени моделирования Т. Выделяют два вида состояний: неособые состояния, в которых система находится почти все время, и особые состояния, характерные для системы в некоторые моменты времени, совпадающие с моментами наступления событий в реальной системе (поступление очередной заявки, освобождение канала и т.д.).
При имитации вторым способом функционирование системы рассматривается как совокупность взаимосвязанных процессов, протекающих параллельно во времени, причем каждый из процессов представляет собой некоторый поток событий. Каждому отдельному событию соответствует изменение состояния системы.
При построении модели системного времени методом особых состояний время меняется в моменты, которые соответствуют моментам наступления событий или, что то же самое, в моменты особых состояний.
Для реализации моделирования по особым состояниям требуется разработка специальной процедуры планирования событий (календаря событий).
Если известен закон распределения интервалов между событиями, то такое прогнозирование труда не составляет: достаточно к текущему значению модельного времени добавить величину интервала, полученную с помощью датчика случайных чисел с соответствующим законом распределения.
Если же момент наступления события определяется некоторыми логическими условиями, то необходимо сформулировать эти условия и проверять их истинность для каждого последующего шага моделирования.
Моделирование по особым состояниям экономичнее и точнее способа фиксированного шага, если:
· события распределены неравномерно и появляются через значительные временные интервалы;
· предъявляются повышенные требования к точности определения взаимного положения событий по времени;
· необходимо учитывать наличие одновременных событий.
Моделирующие алгоритмы для таких систем, построенные по принципу фиксированного шага, оказываются не особенно эффективными. В самом деле, при малом Dt будет затрачено очень много машинного времени на бесполезное определение большого количества неособых состояний. Если же Dt сделать недостаточно малым, появится опасность пропуска некоторых особых состояний, что вообще исключает возможность получения правильных результатов при моделировании. Правда, в некоторых случаях для предотвращения пропуска особых состояний могут быть приняты специальные меры, например, разработаны приемы обнаружения пропуска и возврат к предыдущему моменту времени для повторного прохождения данного интервала с малым Dt.
Т.о. выбор величины шага моделирования является очень важным делом. Универсальной методики решения этой задачи не существует, но во многих случаях можно использовать следующие подходы:
· принимать величину шага равной средней интенсивности возникновения событий различных типов;
· выбирать величину шага равной среднему интервалу между наиболее частыми или наиболее важными событиями.
На практике не всегда строго выдерживается один из перечисленных принципов построения моделирующих алгоритмов. Иногда моделирующие алгоритмы строятся на нескольких принципах одновременно. Например, общая структура моделирующего алгоритма базируется на принципе особых состояний, а между особыми состояниями используется принцип Dt.
Дата добавления: 2015-05-05 ; просмотров: 6 | Нарушение авторских прав



