что такое незамкнутая ломаная
Как выглядит замкнутая ломаная линия
Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.
Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:
Типы ломаных линий
Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.
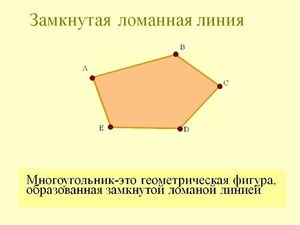
Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.
Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.
Всего существует 4 типа подобных линий по своей структуре:
Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.
Особенности замкнутых линий
Рассмотрим подробнее составляющие части этой геометрической фигуры.
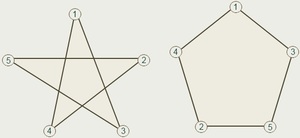
Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.
Многоугольник как разновидность замкнутой ломаной
Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.
Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.
Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.
Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.
У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.
Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.
Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.
Ломаная линия
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Ломаная
Определение 1. Ломаной (ломаной линией) \( \small A_1A_2. A_
Можно дать и другое определение ломаной:
 |
Невырожденная ломаная
Ломаная, описанная в определении 1 называется невырожденной ломаной.
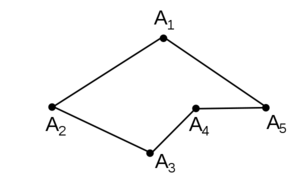
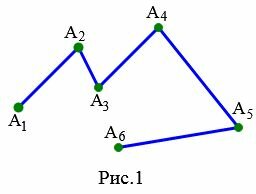
На рисунке 1 ломаная \( \small A_1A_2A_3A_4A_5A_6 \) является невырожденной поскольку отрезки \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\) не лежат на одной прямой.
Вырожденная ломаная
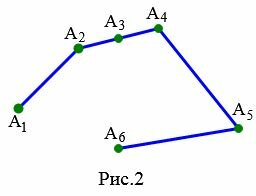 |
На рисунке 2 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \). Эта ломаная является вырожденной поскольку отрезки \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\) лежат на одной прямой.
Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.
Звенья ломаной
Звеньями называют отрезки, из которых состоит ломаная.
Вершины ломаной
Конечные точки звеньев ломаной называются вершинами.
На рисунке 1 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \), состоящая из шести вершин: \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5, \ A_6 \).
Смежные звенья ломаной
Смежные звенья ломаной − это звенья имеющие общую вершину.
На рисунке 3 смежными звеньями ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются звенья: \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\).
Смежные вершины ломаной
Смежными вершинами ломаной называют вершины одного звена ломаной.
На рисунке 3 смежными вершинами ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются вершины: \( \small A_1\) и \( \small A_2\), \( \small A_2\) и \( \small A_3\), \( \small A_3\) и \( \small A_4 \), \( \small A_4\) и \( \small A_5\), \( \small A_5\) и \( \small A_6\).
Незамкнутая ломанная
Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).
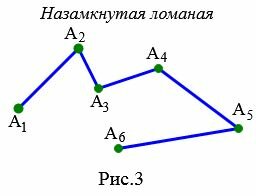 |
Замкнутая ломанная
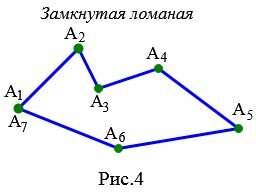 |
На рисунке 4 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) является замкнутым, так как точки: \( \small A_1\) и \( \small A_7\) совпадают и отрезки \( \small A_1A_2\) и \( \small A_6A_7\) не лежат на одной прямой.
Ломаная с самопересечением
Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.
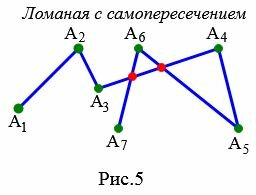 |
Ни рисунке 5 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) имеет самопересечение, так как звенья \( \small A_5A_6 \) и \( \small A_6A_7 \) имеют общие точки со звеном \( \small A_3A_4 \).
Простая ломаная
Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.
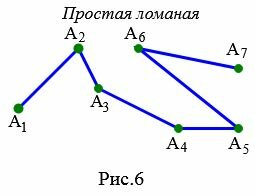 |
Длина ломаной
Длина ломаной равна сумме длин всех звеньев ломаной: \( \small d= A_1A_2+A_2A_3+. +A_
Теорема. Длина ломаной больше расстояния между первым и последним точками.
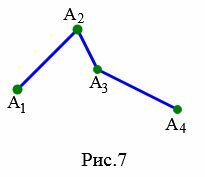 |
Доказательство. Для доказательства теоремы рассмотрим ломаную \( \small A_1A_2A_3A_4 \) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины \( \small A_1, \ A_2, \ A_3 \) не лежат на одной прямой. Тогда имеет место неравенство треугольников:
Для точек \( \small A_1, \ A_3, \ A_4 \) имеет место следующее нестрогое неравенство:
В выражении (2) мы не применяли строгое неравенство поскольку вершины \( \small A_1, \ A_3, \ A_4 \) ломаной не являются соседними вершинами и могут лежать на одной прямой.
В неравенстве (2) вместо слагаемого \( \small A_1 A_3\) подставим сумму \( \small A_1A_2+A_2A_3 \) из (1), которая больше, чем \( \small A_1 A_3\). Тогда получим:
Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками.
Аналогично доказывается теорема для ломанной с любым количеством звеньев.
Точка и линия
Я не буду рассказывать вам, что об этом пишут в различных учебниках, ведь вы здесь для того, чтобы понять и применять, а не для того, чтобы зубрить. Я расскажу так, чтобы было понятно.
Точка – это воображаемый геометрический объект, не имеющий никаких размеров и не состоящий ни из чего.
У точки нет ни длины, ни ширины, ни высоты. Ее нельзя измерить. Точка неделимая. Она не состоит ни из каких-либо других частей.
Зачем нужна точка, если она воображаемая? Для чего ее придумали?
Точка выполняет только одну задачу: указание месторасположения.
Пример: точка на карте навигатора указывает нам на то, где находится конечный пункт поездки, то есть, на его местоположение.
Линия – это множество точек, расположенных последовательно друг за другом.
Например, представим себе цепь. Можно вообразить, что каждое ее звено – это точка. И точно так же, как цепь состоит из звеньев, соединенных между собой, так и линия состоит из точек, образно говоря, склеенных друг с другом.
Рис. 1 Цепь и линия
Линия не имеет ширины и высоты, но можно измерить ее длину. Линия состоит из точек.
Как можно измерить то, что состоит из придуманных объектов, не имеющих размеров? Зачем нужна линия?
Действительно, геометрическая точка не имеет размеров, ее невозможно измерить. Но она, как было сказано выше, указывает на местоположение чего-либо конкретного.
Возьмем для примера опять навигатор. Вы на автомобиле проехали от своего дома в любимое кафе.
Рис. 2 Путь автомобиля
Можем ли мы представить автомобиль точкой? Да, можем. Во время движения автомобиль изменял свое местоположение. Чтобы показать на карте, в каких именно местах побывал автомобиль во время поездки, мы обозначим их точками, следовательно, для упрощения рисунка мы смело можем заменить автомобиль точкой. Тогда полный путь от дома к кафе (множество мест на дороге, на которых побывала машина) мы можем изобразить в виде линии, то есть, идущих друг за другом точек. А так как путь от дома к кафе имеет какую-то длину, то и нарисованная линия имеет длину, равную этому пути, а значит, линию можно измерить.
Рис. 3 Контур и диапазон
Как видно на примере рисунка 3-а, при помощи линии обозначено очертание птицы на ветке, а на 3-б – пример решения неравенств методом интервалов.
Для чего нужна линия:
1. Показывает путь движения какого-либо объекта;
2. С ее помощью можно измерить расстояние между какими-нибудь объектами;
3. Служит для обозначения границ объекта или фигуры;
4. Показывает диапазон каких-то значений.
Обозначение точек и линий
Рис. 4 Обозначение точек и линий
Взаимное расположение точек и линии
Точка может принадлежать линии (то есть, быть одной из ее составляющих), а может не принадлежать ей.
Рис. 4.1 Принадлежность точек линии
При записи на письме точка обозначается при помощи знака точка, заключенного в скобки, с добавлением заглавной буквы латинского алфавита: (·) H
Теперь я запишу то, что мы увидели на рисунке 4.1, на языке геометрии, а вы попробуйте прочитать самостоятельно:
Виды линий
Рис. 5 Замкнутая и незамкнутая линия
Замкнутая линия не имеет обрывающихся концов. Она начинается и заканчивается в одной точке. Причем эта точка может находиться в любом месте на этой линии.
Рис. 6 Контур птицы
Незамкнутая линия имеет один или два обрывающихся конца. Начало и конец такой линии находятся в разных местах (точки A и B ).
Рис. 7 Незамкнутые линии
Еще несколько примеров.
1. Ты вышел из дома погулять и вернулся домой. Какой линией можно обозначить твой путь? Правильно, замкнутой.
2. Ты вышел из дома, погулял, а потом зашел к соседу. Какой линией можно обозначить твой путь? Правильно, разомкнутой.
3. Ты вышел из дома и пошел к другу в дом напротив. Какой линией можно обозначить твой путь? Правильно, разомкнутой.
Также линии бывают:
Рис. 11 Самопересекающиеся и не самопересекающиеся линии
Попробуйте сформулировать самостоятельно, какие линии называются самопересекающиеся, а какие – не самопересекающиеся.
Рис. 12 Прямая, ломаная, кривая линии
Более подробно о прямых, кривых и ломаных линиях рассмотрено в других уроках.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии