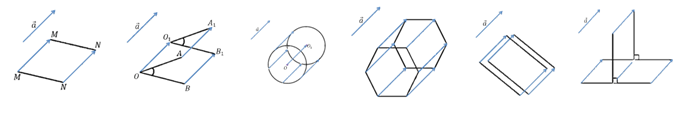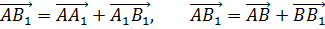что такое параллельный перенос

Параллельный перенос

Урок 11. Геометрия 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Параллельный перенос»

Сегодня на уроке мы вспомним, какое отображение плоскости на себя мы называли параллельным переносом, введём понятие параллельного переноса в пространстве. Проверим, будет ли параллельный перенос движением пространства.

Вернёмся в планиметрию и вспомним, что параллельным переносом мы называли преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние. Мы говорили, что для того, чтобы задать перенос достаточно задать вектор.

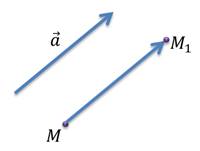
Другими словами, параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка отображается в такую точку , что вектор равен вектору .

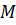
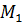
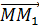
То, что параллельный перенос является примером движения плоскости, мы уже доказывали. Давайте вспомним это доказательство.

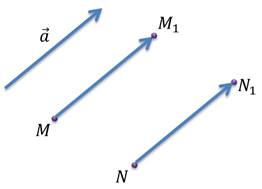
Пусть при параллельном переносе на вектор точки и отображаются в точки и . Так как векторы и , то значит, эти векторы равны между собой . То есть они параллельны и их длины равны, поэтому четырёхугольник – параллелограмм. Следовательно, , то есть расстояние между точками и равно расстоянию между точками и .

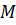
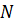
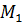
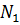
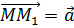
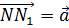
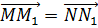
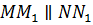
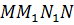
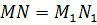
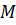
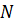
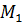
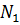
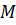
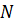
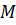
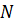
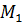
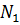
Случай, когда точки и лежат на прямой параллельной вектору , вы можете рассмотреть самостоятельно. Но и в этом случае расстояние между точками и будет равно расстоянию между точками и .

Таким образом, параллельный перенос сохраняет расстояние между точками и поэтому представляет собой движение. Это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

В планиметрии мы говорили, что параллельный перенос обладает некоторыми свойствами.

Свойства параллельного переноса:

· При параллельном переносе отрезок переходит в равный ему отрезок.

· Угол переходит в равный ему угол.

· Окружность переходит в равную ей окружность.

· Любой многоугольник переходит в равный ему многоугольник.

· Параллельные прямые переходят в параллельные прямые.

· Перпендикулярные прямые переходят в перпендикулярные прямые.

Теперь давайте определим, что мы будем понимать под параллельным переносом в пространстве.

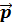
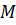
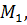
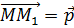
Параллельным переносом на вектор называется такое отображение пространства на себя, при котором любая точка переходит в такую точку что .

Проверим, будет ли параллельный перенос в пространстве примером движения пространства.

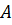
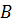
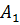
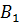
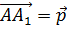
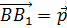
При параллельном переносе точки пространства и переходят в такие точки и , что вектора и .

Сложим по правилу треугольника векторы

Поскольку левые части равенств равны, значит, равны и правые части равенств.

Значит, можно записать, что .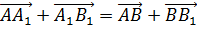

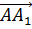
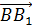
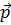
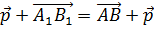
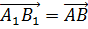
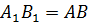
Заменим вектора и на вектор . Получим, что . Отсюда получаем, что вектор . Поскольку векторы равны, значит, равны и их длины, то есть . То есть расстояние между точками при параллельном переносе в пространстве сохраняется, значит, параллельный перенос в пространстве также является движением, но уже не плоскости, а пространства.

Сформулируем свойства параллельного переноса.

Свойства параллельного переноса:

· Параллельный перенос является примером движения пространства.

· При параллельном переносе точки смещаются по параллельным или совпадающим прямым на одно и то же расстояние.

· При параллельном переносе прямая переходит в параллельную прямую (или сама в себя).

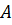
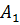
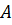
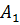
· Каковы бы не были две точки и , существует, и притом единственный, параллельный перенос, при котором точка переходит в точку .

· При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

Движение в пространстве обладает теми же свойствами, что и движение плоскости.

Свойства движения пространства:

· Движение сохраняет расстояние между точками.

· При любом движении пространства отрезок отображается на отрезок, прямая – в прямую, плоскость – в плоскость.

Решим несколько задач.

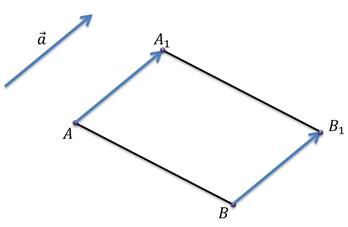
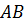
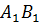
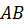
Задача: начертить отрезок и вектор . Построить отрезок , который получится из отрезка параллельным переносом на вектор .

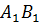
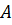
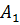
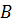
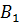
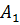
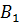
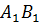
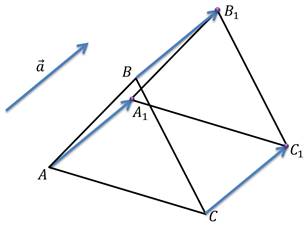
Решение: для того, чтобы построить отрезок , отобразим точку в точку , точку в точку с помощью параллельного переноса. Тогда соединив точки , мы получим отрезок .

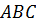
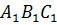
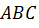
Задача: начертить треугольник и вектор . Построить треугольник , который получится из треугольникa параллельным переносом на вектор .

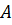
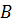
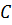
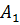
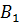
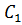
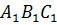
Решение: отобразим с помощью параллельного переноса точки , , в точки , ,. Соединив полученные точки, мы получим искомый треугольник .

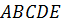
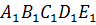
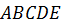
Задача: начертить пятиугольник и вектор . Построить пятиугольник , который получится из пятиугольника параллельным переносом на вектор .

Решение: решать эту задачу будем аналогично тому, как мы решали предыдущую задачу. Отобразим каждую вершину пятиугольника с помощью параллельного переноса на вектор . Соединим получившиеся точки и получим искомый пятиугольник .

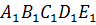
Сегодня на уроке мы вспомнили, что мы понимали под параллельным переносом в планиметрии. Ввели понятие параллельного переноса в пространстве. Сформулировали основные свойства параллельного переноса, движения пространства.

Источник

Параллельный перенос

Урок 11. Геометрия 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Параллельный перенос»

Сегодня на уроке мы вспомним, какое отображение плоскости на себя мы называли параллельным переносом, введём понятие параллельного переноса в пространстве. Проверим, будет ли параллельный перенос движением пространства.

Вернёмся в планиметрию и вспомним, что параллельным переносом мы называли преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние. Мы говорили, что для того, чтобы задать перенос достаточно задать вектор.

Другими словами, параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка отображается в такую точку , что вектор равен вектору .

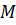
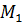
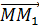
То, что параллельный перенос является примером движения плоскости, мы уже доказывали. Давайте вспомним это доказательство.

Пусть при параллельном переносе на вектор точки и отображаются в точки и . Так как векторы и , то значит, эти векторы равны между собой . То есть они параллельны и их длины равны, поэтому четырёхугольник – параллелограмм. Следовательно, , то есть расстояние между точками и равно расстоянию между точками и .

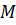
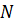
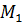
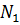
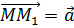
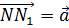
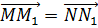
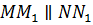
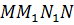
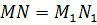
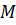
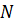
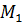
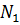
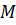
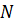
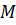
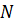
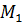
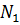
Случай, когда точки и лежат на прямой параллельной вектору , вы можете рассмотреть самостоятельно. Но и в этом случае расстояние между точками и будет равно расстоянию между точками и .

Таким образом, параллельный перенос сохраняет расстояние между точками и поэтому представляет собой движение. Это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

В планиметрии мы говорили, что параллельный перенос обладает некоторыми свойствами.

Свойства параллельного переноса:

· При параллельном переносе отрезок переходит в равный ему отрезок.

· Угол переходит в равный ему угол.

· Окружность переходит в равную ей окружность.

· Любой многоугольник переходит в равный ему многоугольник.

· Параллельные прямые переходят в параллельные прямые.

· Перпендикулярные прямые переходят в перпендикулярные прямые.

Теперь давайте определим, что мы будем понимать под параллельным переносом в пространстве.

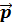
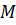
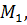
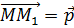
Параллельным переносом на вектор называется такое отображение пространства на себя, при котором любая точка переходит в такую точку что .

Проверим, будет ли параллельный перенос в пространстве примером движения пространства.

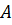
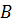
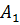
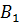
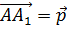
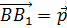
При параллельном переносе точки пространства и переходят в такие точки и , что вектора и .

Сложим по правилу треугольника векторы

Поскольку левые части равенств равны, значит, равны и правые части равенств.

Значит, можно записать, что .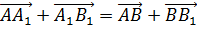

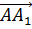
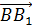
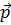
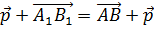
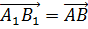
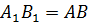
Заменим вектора и на вектор . Получим, что . Отсюда получаем, что вектор . Поскольку векторы равны, значит, равны и их длины, то есть . То есть расстояние между точками при параллельном переносе в пространстве сохраняется, значит, параллельный перенос в пространстве также является движением, но уже не плоскости, а пространства.

Сформулируем свойства параллельного переноса.

Свойства параллельного переноса:

· Параллельный перенос является примером движения пространства.

· При параллельном переносе точки смещаются по параллельным или совпадающим прямым на одно и то же расстояние.

· При параллельном переносе прямая переходит в параллельную прямую (или сама в себя).

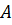
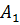
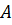
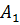
· Каковы бы не были две точки и , существует, и притом единственный, параллельный перенос, при котором точка переходит в точку .

· При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

Движение в пространстве обладает теми же свойствами, что и движение плоскости.

Свойства движения пространства:

· Движение сохраняет расстояние между точками.

· При любом движении пространства отрезок отображается на отрезок, прямая – в прямую, плоскость – в плоскость.

Решим несколько задач.

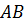
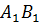
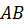
Задача: начертить отрезок и вектор . Построить отрезок , который получится из отрезка параллельным переносом на вектор .

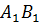
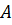
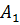
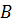
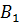
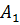
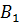
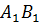
Решение: для того, чтобы построить отрезок , отобразим точку в точку , точку в точку с помощью параллельного переноса. Тогда соединив точки , мы получим отрезок .

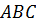
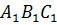
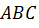
Задача: начертить треугольник и вектор . Построить треугольник , который получится из треугольникa параллельным переносом на вектор .

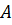
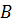
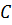
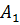
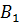
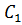
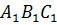
Решение: отобразим с помощью параллельного переноса точки , , в точки , ,. Соединив полученные точки, мы получим искомый треугольник .

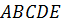
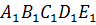
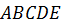
Задача: начертить пятиугольник и вектор . Построить пятиугольник , который получится из пятиугольника параллельным переносом на вектор .

Решение: решать эту задачу будем аналогично тому, как мы решали предыдущую задачу. Отобразим каждую вершину пятиугольника с помощью параллельного переноса на вектор . Соединим получившиеся точки и получим искомый пятиугольник .

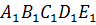
Сегодня на уроке мы вспомнили, что мы понимали под параллельным переносом в планиметрии. Ввели понятие параллельного переноса в пространстве. Сформулировали основные свойства параллельного переноса, движения пространства.

Источник