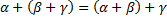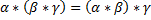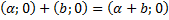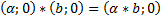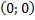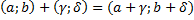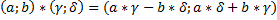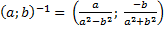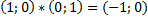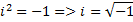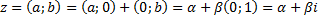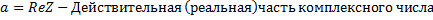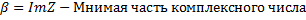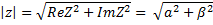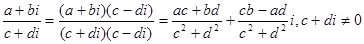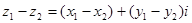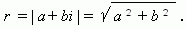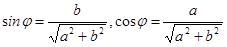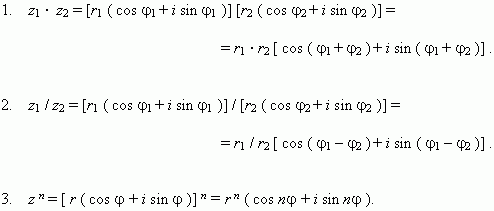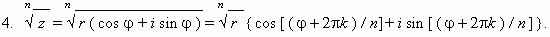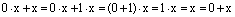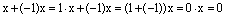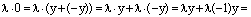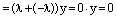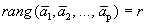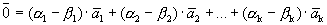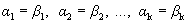что такое поле комплексных чисел
Поле комплексных чисел
Рассмотрим важнейший пример числового поля — поле комплексных чисел.
Два комплексных числа и называются равными, если равны их действительные и мнимые части соответственно:
Сложение и вычитание в поле комплексных чисел
Суммой комплексных чисел и называется комплексное число
Из этого определения и свойств операции сложения действительных чисел следует, что:
а) операция сложения комплексных чисел коммутативна: ;
б) операция сложения комплексных чисел ассоциативна: ;
в) существует нулевой элемент ; нулевой элемент обозначается просто символом нуль ;
г) для каждого комплексного числа существует противоположный ему элемент
Из последнего свойства следует, что на множестве комплексных чисел определена операция вычитания (обратная к сложению). Разностью чисел и называется комплексное число
Умножение и деление в поле комплексных чисел
Произведением комплексных чисел и называется комплексное число
Из определения (В.6) и свойств операции умножения действительных чисел следует, что:
в) существует единичный элемент ; единичный элемент обозначается просто символом единица: ;
Из последнего свойства следует, что на множестве отличных от нуля комплексных чисел определена операция деления (обратная к умножению).
Частным двух чисел и называется комплексное число
Операции сложения и умножения комплексных чисел связаны законом дистрибутивности:
Таким образом, множество комплексных чисел является полем.
Решение. По определению операций получаем
Сопряженные числа в поле комплексных чисел
Из определения следует, что сумма и произведение сопряженных чисел — есть числа действительные:
Используя правила арифметических операций для комплексных чисел, можно установить справедливость свойств операции комплексного сопряжения:
Решение. Пусть — корень уравнения. Тогда
Приравнивая нулю действительную и мнимую части, получаем
3. Из свойств операции комплексного сопряжения следует, что
Введение в комлексные числа
Выяснив, что многие знакомые программисты не помнят комплексные числа или помнят их очень плохо, я решил сделать небольшую шпаргалку по формулам.
А школьники могут что-то новое узнать 😉
// Всех кого заинтересовал прошу под кат.
Итак, комплексные числа эта такие числа, которые можно записать как
Где x, y вещественные числа(т.е привычные всем числа), а i — число, для которого
выполняется равенство
x называется действительной частью, y — мнимой.
Это алгебраическая форма записи комплексного числа.
Существует также тригонометрическая форма записи комплексного числа z:
С введением, пожалуй, все.
Переходим к самому интересному — операциям над комплексными числами!
Для начала рассмотрим сложение.
У нас есть два таких комплексных числа:
Как же их сложить?
Очень просто: сложить действительную и мнимую части.
Получим число:
Все просто, не так ли?
Вычитание выполняется аналогично сложению.
Нужно просто вычесть из действительной части 1 числа действительную часть 2 числа,
а потом проделать тоже с мнимой частью.
Получим число
Умножение выполняется вот так:
Напомню, x это действительная часть, y — мнимая.
Деление выполняется вот так:
Кстати, поддержка комплексных чисел есть в стандартной библиотеке Python:
Вместо i используется j.
Кстати, это потому что Python принял конвенцию инженеров-электриков, у которых
буква i обозначает электрический ток.
Задавайте свой вопросы, если они есть, в комментариях.
Надеюсь, вы узнали для себя что-то новое.
UPD: В комментариях просили рассказать о практическом применении.
Так вот комплексные числа нашли широкое практическое применение в авиации
(подъемная сила крыла) и в электричестве.
Как видете, очень нужная вещь 😉
Поле комплексных чисел



Теорема 1. Множество комплексных чисел С с операциями сложения и умножения образует поле. Свойства сложения
1) Коммутативность:(a+bi)+(c+di)=(a+c)+(b+d)i=(c+di)+(a+bi).
2) Ассоциативность :[(a+bi)+(c+di)]+(e+fi)=(a+c+e)+(b+d+f)i=(a+bi)+[(c+di)+(e+fi)].
3) Существование нейтрального элемента:(a+bi)+(0+0i)=(a+bi). Число 0+0i будем называть нулём и обозначать 0.
4) Существование противоположного элемента: (a+bi)+(–a–bi)=0+0i=0.
5) Коммутативность умножения: (a+bi)(c+di)=(ac–bd)+(bc+ad)i=(c+di)(a+bi).
6) Ассоциативность умножения:если z1=a+bi, z2=c+di, z3=e+fi, то (z1z2)z3 =z1(z2z3).
7) Дистрибутивность: если z1=a+bi, z2=c+di, z3=e+fi, то z1(z2+z3)=z1z2+z1z3.
8) Нейтральный элемент для умножения:(a+bi)(1+0i)=(a·1–b·0)+(a·0+b·1)i=a+bi.
9) Число 1+0i=1 – единица.
Если b=0, то z=a+ 0i=a– действительное число. Поэтому множество действительных чисел Rявляется частью множества комплексных чисел C: R Í C.
Заметим: i 2 =(0+1i)(0+1i)=–1+0i=–1. Используя это свойство числа i, а также свойства операций, доказанные в теореме 1, можно выполнять действия с комплексными числами по обычным правилам, заменяя i 2 на –1.
2 Тригонометрическая форма записи.
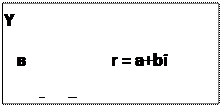



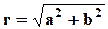
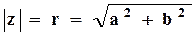
Полярный угол j называется аргументом числа z: 
Аргумент определяется с точностью до слагаемого 2kp; значение, для которого –p
Глава 5. Поле комплексных чисел С
Непустое множество К с бинарными операциями сложения и умножения называется полем(числовым полем), если выполнены следующие аксиомы:
0) Бинарные операции сложения и умножения являются замкнутыми.
1) Бинарные операции сложения и умножения являются коммутативными
2) Бинарные операции являются ассоциативными:
3) Имеет место закон дистрибутивности умножения относительно сложения.
4) Каждый ненулевой элемент имеет себе обратный, и каждый элемент имеет себе противоположный.
5) Общая группа аксиом связанных с другими свойствами элементов.
Рассмотрим поле действительных чисел R и на его основе рассмотрим множество всевозможных, упорядоченных пар вида (а,0) для которых выполняются законы:
1)
2)
3) Роль единичного элемента играет пара вида 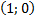
Получается множество, состоящее из объектов отличных от действительных чисел, для которых выполнены все законы действительных чисел (включая законы 1-3 выше)
Таким образом поле действительных чисел R и новое множество являются изоморфными.
Теперь рассмотри множество всех упорядоченных пар вида
Возникает вопрос, будет ли данное множество изоморфно множеству чисел R.
Такое множество найти МОЖНО. (Он сам велел дофига знаков поставить)
Нужно лишь для пар 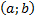
1)
2)
3)
4) Роль единичного элемента играет пара вида 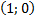
5) Особую роль единичного элемента играет пара вида (0;1)
Перемножим
То есть квадрат элемента (0;1) равен отрицательному числу..(. )
Поэтому пара (0;1) обозначается I и называется «мнимой единицей» для которой имеет место
Множество всех упорядоченных пар 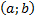
Алгебраическая форма комплексного числа
Модули комплексного числа z называется величина
Комплексное число 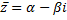
Теорема об отношениях сравнения на поле комплексных чисел С:
Поле комплексных чисел не является упорядоченным, то есть сравнивать 2 комплексных числа с помощью бинарного отношения типа сравнения (
Поле комплексных чисел. Геометрическое представление комплексных чисел и операции над ними. Тригонометрическая форма комплексного числа
Комплексным числом zназ. выражение 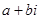
При этом выполняются соглашения:
1) с выражением a+bi можно производить арифметические операции по правилам, которые приняты для буквенных выражений в алгебре;
5) равенство a+bi=c+di, где a, b, c, d – действительные числа, имеет место тогда и только тогда, когда a=c и b=d.
Число 0+bi=bi называется мнимым или чисто мнимым.
Любое действительное число а есть частный случай комплексного числа, ведь его можно записать в виде a=a+ 0i. В частности, 0=0+0i, но тогда ели a+bi=0, то a+bi=0+0i, следовательно, a=b=0.
Т.о., комплексное число a+bi=0 тогда и только тогда, когда a=0 и b=0.
Из соглашений следуют законы преобразования комплексных чисел:
Мы видим, что сумма, разность, произведение и частное (где делитель не равен нулю) комплексных чисел, в свою очередь комплексное число.
Число а наз. вещественной частью комплексного числа z (обозначается 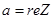
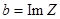
Комплексное число z с нулевой вещественной частью наз. чисто мнимым, с нулевой мнимой – чисто вещественным.
Два комплексных числа наз.равными,если у них совпадают и вещественная и мнимая части.
Два комплексных числа наз. сопряженными, если у них веществ. части совпадают, а мнимые отличаются знаками. 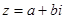
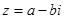
Сумма сопряженных чисел есть число веществ, а разность чисто мнимое число. На множестве комплексных чисел естественным образом определены операции умножения и сложения чисел. Именно, если 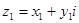
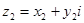
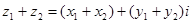
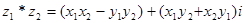
Определим теперь операции вычитания и деления.
Заметим, что произведение двух комплексных чисел есть число веществ.
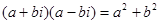
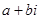
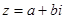
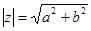
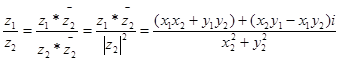
В отличие от вещественных чисел для комплексных чисел не вводится понятие «больше», «меньше».
Геометрическое представление комплексных чисел.Действительные числа изображаются точками на числовой прямой:
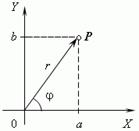
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (рис.). Эта система координат называется комплексной плоскостью.
Модулемкомплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
Сопряжённые комплексные числа имеют одинаковый модуль. __
Тригонометрическая формакомплексного числа. Наряду с записью комплексного числа в алгебраической форме также употребляется и другая, называемая тригонометрической.
Пусть комплексное число z=a+bi изображается вектором ОА с координатами (a,b). Обозначим длину вектора ОА буковой r: r=|ОА|, а угол, который он образует с положительным направлением оси Ох – через угол φ.
Воспользовавшись определениями функций sinφ=b/r, cosφ=a/r, комплексное число z=a+bi можно записать в виде z=r(cosφ+i*sinφ), где 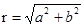
Тригонометрической формой комплексного числа z называется его представление в виде z=r(cosφ+i*sinφ), где r и φ – действительные числа и r≥0.
Действительно число r называется модулем комплексного числа и обозначается |z|, а угол φ – аргументом комплексного числа z. Аргумент φ комплексного числа z обозначается Arg z.
Операции с комплексными числами, представленными в тригонометрической форме:
Это знаменитая формула Муавра.
8.Векторное пространство. Примеры и простейшие свойства векторных пространств. Линейная зависимость и независимость системы векторов. Базис и ранг конечной системы векторов
Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа. В применении к любым векторам х, у, z и любым числам α, β эти правила удовлетворяют следующим условиям:
3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x+0=x: для любого вектора x;
4) для любого вектора х существует противоположный ему вектор у такой, что х+у =0,
6) α(βx)=(αβ)х (ассоциативность умножения), где произведение αβ есть произведение скаляров
7) (α+β)х=αх+βх (распределительное свойство относительно числового множителя);
8) α(х+у)=αх+αу(распределительное свойство относительно векторного множителя).
Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям 1-8.
Примерами таких пространств могут служить множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д.
Теорема “Простейшие свойства векторных пространств”
1. В векторном пространстве существует единственный нулевой вектор.
2. В векторном пространстве любой вектор имеет единственный противоположный ему.
3. 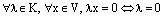
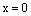
4. 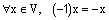
Док-во
Пусть 0 – нулевой вектор векторного пространства V. Тогда 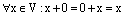
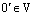
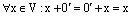
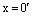
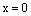
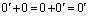
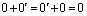
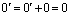
Сначала мы докажем, что произведение нулевого скаляра на любой вектор равен нулевому вектору.
Пусть 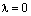
Относительно сложения векторное пространство является абелевой группой, а в любой группе справедлив закон сокращения. Применяя закон сокращения, из последнего равенства следует 0*х=0
Теперь докажем утверждение 4). Пусть 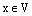
Отсюда сразу же следует, что вектор (-1)х является противоположным вектору х.
Пусть теперь х=0. Тогда, применяя аксиомы векторного пространства, 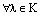

Пусть 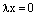
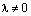
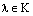
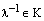
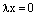
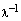
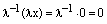
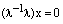
Линейная зависимость и независимость системы векторов. Набор векторов 
Система из 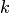

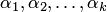
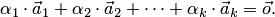
Система из k векторов 
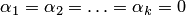
Замечания:
1. Один вектор 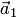
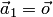
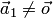
2. Любая часть системы векторов называется подсистемой.
Свойства линейно зависимых и линейно независимых векторов:
1. Если в систему векторов входит нулевой вектор, то она линейно-зависима.
2. Если в системе векторов имеется два равных вектора, то она линейно-зависима.
3. Если в системе векторов имеется два пропорциональных вектора 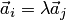
4. Система из k>1 векторов линейно-зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
5. Любые векторы, входящие в линейно-независимую систему, образуют линейно-независимую подсистему.
6. Система векторов, содержащая линейно-зависимую подсистему, линейно-зависима.
7. Если система векторов 
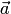
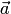

Тогда из равенства 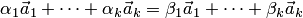
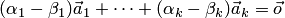
Следовательно, линейная комбинация векторов 
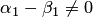

Ранг и базис системы векторов. Рангом системы векторов называется максимальное число линейно-независимых векторов системы.
Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
Теорема. Любой вектор системы можно представить в виде линейной комбинации векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.
Док-во:
Пусть система 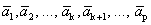
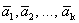
1 случай. Вектор 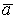
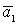
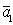
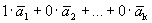
2 случай. Вектор 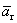
Рассмотрим систему векторов 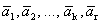
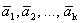
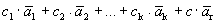
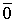
Очевидно, что 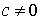
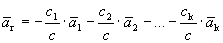
Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.
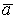
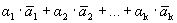
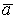
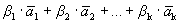
Вычитая эти равенства, получим
Учитывая линейную независимость векторов базиса, получим
Следовательно, разложение вектора по базису единственно.
Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.